Advent of Code 2024 [Days 6 to 8]

January 18, 2025   ·   AoC   C++   ·   Advent of Code

Advent of Code 2024 [Days 6 to 8]

Welcome Back!. I’ve decided to use Advent of Code 2024 as a platform to improve my C++ skills, and in the previous part I covered Days 1 to 5.

This is my attempt to document my learning journey through Advent of Code 2024. Instead of cluttering with each post for each day’s challenge, I’ll be grouping my progress into consolidated posts. This page is the second part of my progress log covering Days 6 to 8.

Full solutions are available on GitHub: ABD-01/AoC2024.

Day 6: Guard Gallivant

Solution Overview

void Guard::move(std::vector<std::string>& map)
{
    map[position.x][position.y] = 'X';
    Point temp = position+direction;

    if (temp.x < 0 || temp.y < 0 || temp.x >= map.size() || temp.y >= map[0].size())
    {
        can_move = false;
        cout << "Guard left the map" << endl;
        return;
    }

    if (map[temp.x][temp.y] == '#' || map[temp.x][temp.y] == 'O')
    {
        // Guard hit an obstacle, turn right
        turnRight();
        move(map);
        return;
    }

    if(is_looping(temp, direction))
    {
        can_move = false;
        stuck_in_loop = true;
        cout << "Guard stuck in a Loop" << endl;
        return;
    }

    position = temp;

    visited.emplace(position, direction);
}

void Guard::turnRight()
{
    //-1,0  -> 0,1
    // 0,1  -> 1,0
    // 1,0  -> 0,-1
    // 0,-1 -> -1,0
    direction = Point(direction.y, -direction.x);
}

bool Guard::is_looping(Point p, Point d) const
{
    PointMap::const_iterator it = visited.find(p);
    if (it != visited.end() && it->second == d)
        return true;
    return false;
}

Part 1: Predict the Guard’s Route

The Guard moves in a 2D grid, turning right upon hitting an obstacle (# or O). The goal is to find the number of distinct positions visited before the Guard exits the map. Key Logic:

• Create an unordered set (\(O(1)\) insert) for visited positions.

• If using a vector, check for duplicates before inserting (\(O(n)\)).

• Move the Guard until it exits the map.

• On obstacle collision → turn right → retry movement.

• Return visited.size() for number of distinct positions.

Part 2: Trap the Guard in a Loop

You need to get the guard stuck in a loop by adding a single new obstruction. How many different positions could you choose for this obstruction?

Brute force solution would be to iterate over all possible position on the map. A better solution would be to only place obstacles on path that the guard travels.

• Created an unordered_map to store each visited position with its corresponding direction. (visited.emplace(position, direction))

• A loop occurs on visiting same position and have same direction as before

using PointMap = std::unordered_map<Point, Point, PointHash>;
...

    PointMap guardVisitedPositions = g.getVisited();  // from part 1
    for(const std::pair<Point, Point>& v: guardVisitedPositions)
    {
        int i(v.first.x), j(v.first.y);
        
        if(i==gx && j==gy) continue;
        
        map[i][j] = 'O';
        g = Guard(Point(gx, gy), Guard::dirUp);
        
        while (g.canMove())
        {
            g.move(map);
        }
        if(g.stuckInLoop())
        {
            ++numObstacles;
        }
        map[i][j] = 'X';
    }

Concepts Learned

Operator Overload

Example Operator Overloading for Point Class

struct Point
{
    int x,y;
    Point(int x, int y): x(x), y(y) {}

    Point operator+(const Point& p)
    {
        return Point(x + p.x, y + p.y);
    }
    bool operator==(const Point& p) const
    {
        return x == p.x && y == p.y;
    }

}
std::ostream& operator<<(std::ostream& os, const Point& p)
{
    os << "(" << p.x << ", " << p.y << ")";
    return os;
}

const Correctness

We bind type modifiers and qualifiers to the left

—Modern C, Jens Gustedt (Page 18)

1. const X* p

   const int* p;  // p points to a constant int (can't modify the value it points to)
   int a = 5;
   p = &a;  // okay, p can point to another int
   *p = 10;  // error, can't modify the value of a through p
   

2. X const* p

   int const* p;  // Same as `const int* p`
   

3. X* const p

   int* const p = &a;  // p is a constant pointer, it always points to the same location
   *p = 10;  // okay, the value of the object p points to can be modified
   p = &b;  // error, can't change p to point to another object
   

4. const X* const p

   const int* const p = &a;  // p is a constant pointer to a constant int
   *p = 10;  // error, can't modify the value of the object p points to
   p = &b;  // error, can't change p to point to another object
   

5. The const at the end of member function does not modify the state of object.

class Fred {
public:
  void inspect() const;   // This member promises NOT to change *this
  void mutate();          // This member function might change *this
};
void userCode(Fred& changeable, const Fred& unchangeable)
{
  changeable.inspect();   // Okay: doesn't change a changeable object
  changeable.mutate();    // Okay: changes a changeable object
  unchangeable.inspect(); // Okay: doesn't change an unchangeable object
  unchangeable.mutate();  // ERROR: attempt to change unchangeable object
}

6. const Point& Return type

class Guard
{
public:
    // Getter functions to access position and direction
    const Point& getPosition() const { return position; }
    const Point& getDirection() const { return direction; }
    /**
    By returning a constant reference (const Point&), you provide read-only access to the position and direction. 
    This ensures that the caller cannot modify the values.
    */

Dangling References

const int& getTemp() {
    int temp = 10;  // Local variable
    return temp;  // Dangling reference (temp goes out of scope)
}

Point p1(1, 2);
const int& a = p1.getX();
p1 = Point(3, 4);  // a now refers to a destroyed object!

In C++, there is no built-in way to directly check if a reference is dangling

Unordered set

Used Hash Table to store elements Steps to use unordered_set with a custom class:

1. Define a hash function for your Point class.

2. Override == operator to check for equality, as unordered_set uses it to compare elements.

3. Use the custom hash function in unordered_set.

Example Code

struct Point
{
    int x,y;
    Point(int x, int y): x(x), y(y) {}
    Point() : x(0), y(0) {}

    Point operator+(const Point& p) const
    {
        return Point(x + p.x, y + p.y);
    }
    bool operator==(const Point& p) const
    {
        return x == p.x && y == p.y;
    }
};
struct HashPoint {
    std::size_t operator()(const Point& p) const {
        return std::hash<int>()(p.x) ^ (std::hash<int>()(p.y) << 1);
    }
};
std::unordered_set<Point, HashPoint> visited;

For unordered_set of std::pair<Point, Point>

Code

// Define a custom hash for std::pair<Point, Point>
struct PairHash {
    size_t operator()(const std::pair<Point, Point>& pair) const {
        PointHash pointHash;
        // Combine the hash values of the two points in the pair
        return pointHash(pair.first) ^ (pointHash(pair.second) << 1);
    }
};

// Overload equality operator for std::pair<Point, Point>
struct PairEqual {
    bool operator()(const std::pair<Point, Point>& a, const std::pair<Point, Point>& b) const {
        return a.first == b.first && a.second == b.second;
    }
};
/** This can also be omitted
The == operator for std::pair is already defined (since std::pair is a standard library type).
It compares both elements of the pair for equality.
*/

std::unordered_set<std::pair<Point, Point>, PairHash, PairEqual> pointPairs;
std::unordered_set<std::pair<Point, Point>, PairHash> point_pairs;

// Aliases 
using PointSet = std::unordered_set<Point, PointHash>;
using PointPairSet = std::unordered_set<std::pair<Point, Point>, PairHash>;

Unordered Map

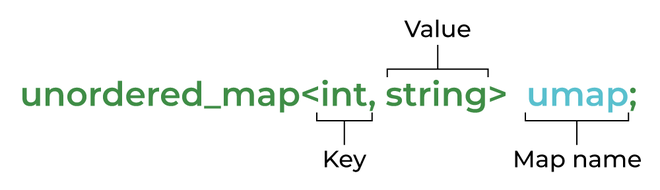
std::unordered_map<Point, Point, PointHash> visited;

// ### Check if value is in HashMap
std::map<char,int> mymap;
std::map<char,int>::iterator it;

if (visited.find(current) != visited.end() && visited[current] == direction) {
    return true; 
}
// If current is not already in the map, accessing visited[current] will insert a new entry

auto it = visited.find(current);
if (it != visited.end() && it->second == direction) {
    return true; 
}

// ### Looping through HashMap
for(const std::pair<Point, Point>& v: visited)
{
    cout << v.first << ":" << v.second << endl;
}

Static Constant Members in C++ Classes

• static const is used for class-level constants, meaning these constants are shared across all instances of the class.

• The static keyword ensures the constant is a class-wide (not instance-specific) member, while const ensures the values cannot be modified.

• Static members must be defined outside the class, even if they’re const.

• You cannot initialize static members within constructors. Integral types you can initialize inline at their declaration.

class Guard{
public:
    static const Point dirUp, dirDown, dirLeft, dirRight;
    static const int a = 4; // works
};
const Point Guard::dirUp(-1, 0);
const Point Guard::dirDown(1, 0);
const Point Guard::dirLeft(0, -1);
const Point Guard::dirRight(0, 1);

References and Resources

• c++ - What is the meaning of ‘const’ at the end of a member function declaration? - Stack Overflow

• Const Correctness, C++ FAQ

• The C++ ‘const’ Declaration: Why & How

• How to create an unordered_set of user defined class or struct in C++? - GeeksforGeeks or unordered set - How can I use a C++ unordered_set for a custom class? - Stack Overflow

• hash - C++ unordered_map using a custom class type as the key - Stack Overflow

• c++ - How do you loop through a std::map? - Stack Overflow

• How to initialize a “static const” data member in C++? - Stack Overflow

• ChatGPT

---

Day 7: Bridge Repair

Solution Overview

Part 1: Given a test value and a list of numbers, determine whether the numbers can be combined using the operators + (addition) and * (multiplication) to produce the test value

Operators are always evaluated left-to-right, not according to precedence rules.

Part 2: Introduces a third operator: concatenation (||), alongside + and *.

Using a recursive call, with using one operator from left at each call.

using ll = long long;

bool check_target1(const std::vector<int>& operands, int index, ll current_value, ll target)
{
    // reached end and found thr test value
    if(index==(int)operands.size()) return current_value == target;

    // If current value is already greater than the target, no point in continuing
    // small improvement by short circuiting
    if(current_value > target) return false;

    // subtle Bug! You only want to check for equality when list is exhausted
    //if(current_value == target) return true;

    return check_target1(operands, index+1, current_value + operands[index], target) 
        || check_target1(operands, index+1, current_value * operands[index], target);
}

bool check_target2(const std::vector<int>& operands, int index, ll current_value, ll target)
{
    if(index==(int)operands.size()) return current_value == target;

    if(current_value > target) return false;

    return check_target2(operands, index+1, current_value + operands[index], target) 
        || check_target2(operands, index+1, current_value * operands[index], target)
        || check_target2(operands, index+1, concat(current_value, operands[index]), target);
}

void part(const std::vector<std::pair<ll, std::vector<int>>>& data)
{
    ll result = 0;
    for(const std::pair<ll, std::vector<int>>& d: data)
        if(check_target(d.second, 0, 1, d.first))
}

The time complexity is \(O(n^2)\) for Part 1and \(O(n^3)\) for Part 2. While this works, it can be optimized.

Optimization

With each recursive call the current_value increases. One way to optimize is to process the operations in reverse order, starting from the right, and try to undo the operations to see if the target value can be constructed. resulting in current value to be 0 at the end.

For example: Given 292: 11 6 16 20, the goal is to check if 292 can be made from these numbers. The left-to-right approach:

• [11+6, 16, 20] → [17*16, 20] → [292] The right-to-left approach:

• [11, 6, 16, 292-20] → [11, 6, 272/16] → [11, 17-6] → [11-11] → [0] To undo concatenation (||), the check_int_contains function is used to check if an integer is present in another integer.

bool check_target1_v2(const std::vector<int>& operands, int index, ll target)
{
    if(index < 0) return target == 0 || target == 1;

    if(target < 0) return false;

    if(target % operands[index] == 0)
    {
        if(check_target1_v2(operands, index-1, target/operands[index]))
            return true;
        // Here too there can be a subtle Bug
        // if you return check_target1_v2(i-1, target/operands[i])
        // it fails to account for check_target1_v2(i-1, target-operands[i])
        // example: 103304: 269 4 96 8
    }

    return check_target1_v2(operands, index-1, target-operands[index]);
}
bool check_int_contains(ll target, ll subint, ll& new_target)
{
    int lt, ls;
    while(subint > 0)
    {
       lt = target % 10;
       target /= 10;
       ls = subint % 10;
       subint /= 10;
       if(lt != ls)
       {
           return false;
       }
    }
    new_target = target;
    return true;
}

bool check_target2_v2(const std::vector<int>& operands, int index, ll target)
{
    if(index < 0) return target == 0 || target == 1;

    if(target < 0) return false;

    if(target % operands[index] == 0)
    {
        if(check_target2_v2(operands, index-1, target/operands[index]))
            return true;
    }
    
    ll new_target;
    if(check_int_contains(target, operands[index], new_target))
    {
        if(check_target2_v2(operands, index-1, new_target))
            return true;
    }

    return check_target2_v2(operands, index-1, target-operands[index]);
}

While the time complexity still remains the same, there is significant improvement in the time taken. {emphasize-lines=”5,7,9,11”}

[100%] Linking CXX executable day7.exe
Copying input.txt to input7.txt
[100%] Built target day7
Part 1: 6392012777720
Elapsed time: 2283 us
Part 2: 61561126043536
Elapsed time: 121022 us
Part 1 (Version 2): 6392012777720
Elapsed time: 1268 us
Part 2 (Version 2): 61561126043536
Elapsed time: 1498 us
[100%] Built target run7

Concepts Learned

Subsets of an array/vector using bit manipulation

• For an array of size \(n\), there are \(2^n\) possible subsets.

• Each subset corresponds to a binary number between 0 and \(2^n - 1\).

Example

// ### Problem: Find All Subsets That Sum to a Target Value
#include <iostream>
#include <vector>
using namespace std;

void findSubsetsThatSumToTarget(vector<int>& nums, int target) {
    int n = nums.size();
    vector<vector<int>> result;

    // Iterate over all possible subsets
    for (int mask = 0; mask < (1 << n); mask++) {
        vector<int> subset;
        int sum = 0;

        // Generate the subset for the current bitmask
        for (int i = 0; i < n; i++) {
            if (mask & (1 << i)) { // If the i-th bit is 1, include nums[i]
                subset.push_back(nums[i]);
                sum += nums[i];
            }
        }

        // Check if the subset sum equals the target
        if (sum == target) {
            result.push_back(subset);
        }
    }

    // Print the result
    cout << "Subsets that sum to " << target << ":\n";
    for (auto& subset : result) {
        cout << "[ ";
        for (int num : subset) {
            cout << num << " ";
        }
        cout << "]\n";
    }
}

int main() {
    vector<int> nums = {2, 3, 5};
    int target = 5;
    findSubsetsThatSumToTarget(nums, target);
    return 0;
}

References and Resources

• Print all subsets of a given Set or Array - GeeksforGeeks

• Binary Tree Target Check - ChatGPT

---

Day 8: Resonant Collinearity

Solution Overview

The grid is parsed into a dictionary (unordered_map<char, vector<Vec2<int>>>) with antenna labels as the key and a list of all the label’s positions as values.

Part 1: Find the Antinodes

an antinode occurs at any point that is perfectly in line with two antennas of the same frequency - but only when one of the antennas is twice as far away as the other.

The words are complicated, see the diagram below. Basically, an antinode is a point that lies on the line extending from a pair of antennas at an equal distance beyond one of them

..........
...#......
..........
....a.....
..........
.....a....
..........
......#...
..........
..........

Logic:

• iterate over each pair of antennas with the same frequency.

• for each pair, compute the distance between the two antennas and calculate the potential antinode positions on either side of the pair.

• Check if the antinodes lie within the grid boundaries, and if they do, add them to an unordered_set to ensure uniqueness.

std::unordered_set<int> antinodes;
for(const std::pair<const char, std::vector<V2>>& antenas: data)
{
    const std::vector<V2>& a = antenas.second;
    for(int i = 0; i < static_cast<int>(a.size()); ++i)
    {
        for (int j = i + 1; j < static_cast<int>(a.size()); ++j)
        {
            // Calculate distance and antinode positions
            V2 dist = a[i] - a[j];
            V2 antinode1(a[i] + dist), antinode2(a[j] - dist);
            
            // Check if antinode positions are within bounds
            if(antinode1.x < maxX && antinode1.y < maxY && antinode1.x >= 0 && antinode1.y >= 0)
            {
                antinodes.insert(antinode1.x * maxY + antinode1.y);
            }
            if(antinode2.x < maxX && antinode2.y < maxY && antinode2.x >= 0 && antinode2.y >= 0)
            {
                antinodes.insert(antinode2.x * maxY + antinode2.y);
            }
        }
    }
}

To track the unique antinode positions, we need to map each (x, y) coordinate to a unique integer value. This is done by using a simple mathematical formula: antinode1.x*maxY + antinode1.y

Part 2: I mean Harmonic Antinodes

it turns out that an antinode occurs at any grid position exactly in line with at least two antennas of the same frequency, regardless of distance. This means that some of the new antinodes will occur at the position of each antenna (unless that antenna is the only one of its frequency).

Again, the words doesn’t explain much, see the diagram. Similar to Part 1, but instead of stopping at the first antinode, continue along the line of collinearity to count all antinodes.

T....#....
...T......
.T....#...
.........#
..#.......
..........
...#......
..........
....#.....
..........

Logic:

• for each pair, compute the distance between the two antennas and calculate the potential antinode positions on either side of the pair.

• expand the antinode positions by moving along the calculated distance in both directions until we reach the boundary of the grid.

while(antinode1.x < maxX && antinode1.y < maxY && antinode1.x >= 0 && antinode1.y >= 0)
{
    antinodes.insert(antinode1.x * maxY + antinode1.y);
    antinode1 += dist;  // Move along the distance
}
while(antinode2.x < maxX && antinode2.y < maxY && antinode2.x >= 0 && antinode2.y >= 0)
{
    antinodes.insert(antinode2.x * maxY + antinode2.y);
    antinode2 -= dist;  // Move along the distance
}

Concepts Learned

Operator Overloading for custom class

Operator overloading to work with the custom Vec2 class representing a 2D vector. This allows to simplify the code when working with positions and distances, such as adding, subtracting, or comparing positions.

Example

template <typename T>
struct Vec2
{
    T x, y;
    Vec2(T x_val, T y_val) : x(x_val), y(y_val) {}
};

using V2 = Vec2<int>;
using mapV2 = std::unordered_map<char, std::vector<Vec2<int>>>;

template <typename T> Vec2<T> constexpr operator+(Vec2<T> a, Vec2<T> b) { return {a.x + b.x, a.y + b.y}; }
template <typename T> Vec2<T> constexpr operator-(Vec2<T> a, Vec2<T> b) { return {a.x - b.x, a.y - b.y}; }
template <typename T> Vec2<T> constexpr operator-(Vec2<T> a) { return {-a.x, -a.y}; }
template <typename T> Vec2<T> constexpr operator*(Vec2<T> a, Vec2<T> b) { return {a.x * b.x, a.y * b.y}; }
template <typename T> Vec2<T> constexpr operator*(Vec2<T> a, T b) { return {a.x * b, a.y * b}; }
template <typename T> Vec2<T> constexpr &operator+=(Vec2<T> &a, Vec2<T> b) { a = a + b; return a; }
template <typename T> Vec2<T> constexpr &operator-=(Vec2<T> &a, Vec2<T> b) { a = a - b; return a; }
template <typename T> bool constexpr operator==(Vec2<T> a, Vec2<T> b) { return a.x == b.x && a.y == b.y; }
template <typename T>
std::ostream& operator<<(std::ostream& os, const Vec2<T>& v)
{
    os << "(" << v.x << "," << v.y << ")";
    return os;
}

template <typename T>
std::ostream& operator<<(std::ostream& os, const std::vector<T>& v)
{
    os << "[";
    for (auto i = v.begin(); i != v.end(); ++i) {
        if (i != v.begin()) os << ", ";
        os << *i;
    }
    os << "]";
    return os;
}

Constexpr

Enable compile-time evaluation of simple functions, improving performance. # TODO: write in detail

this pointer

# TODO

Unique Number for each element in 2D grid

for \(arr[i][j]\) \(\rightarrow\) \(i\times Cols + j\), where \(Cols\) is number of columns.

---

This marks the second part of my Advent of Code 2024 journey. More updates soon. If you’re also learning C++ or participating in Advent of Code, I’d love to hear about your experiences! Share your thoughts, tips, or solutions in the comments below. Feel free to check out my solutions on GitHub.

Learning CPP via Advent of Code 2024 [Days 1 to 5] Learning CPP via Advent of Code 2024 [Day 9]

Comments