Chapter 1 | The Beauty of Graph Theory#
03:07
03:05
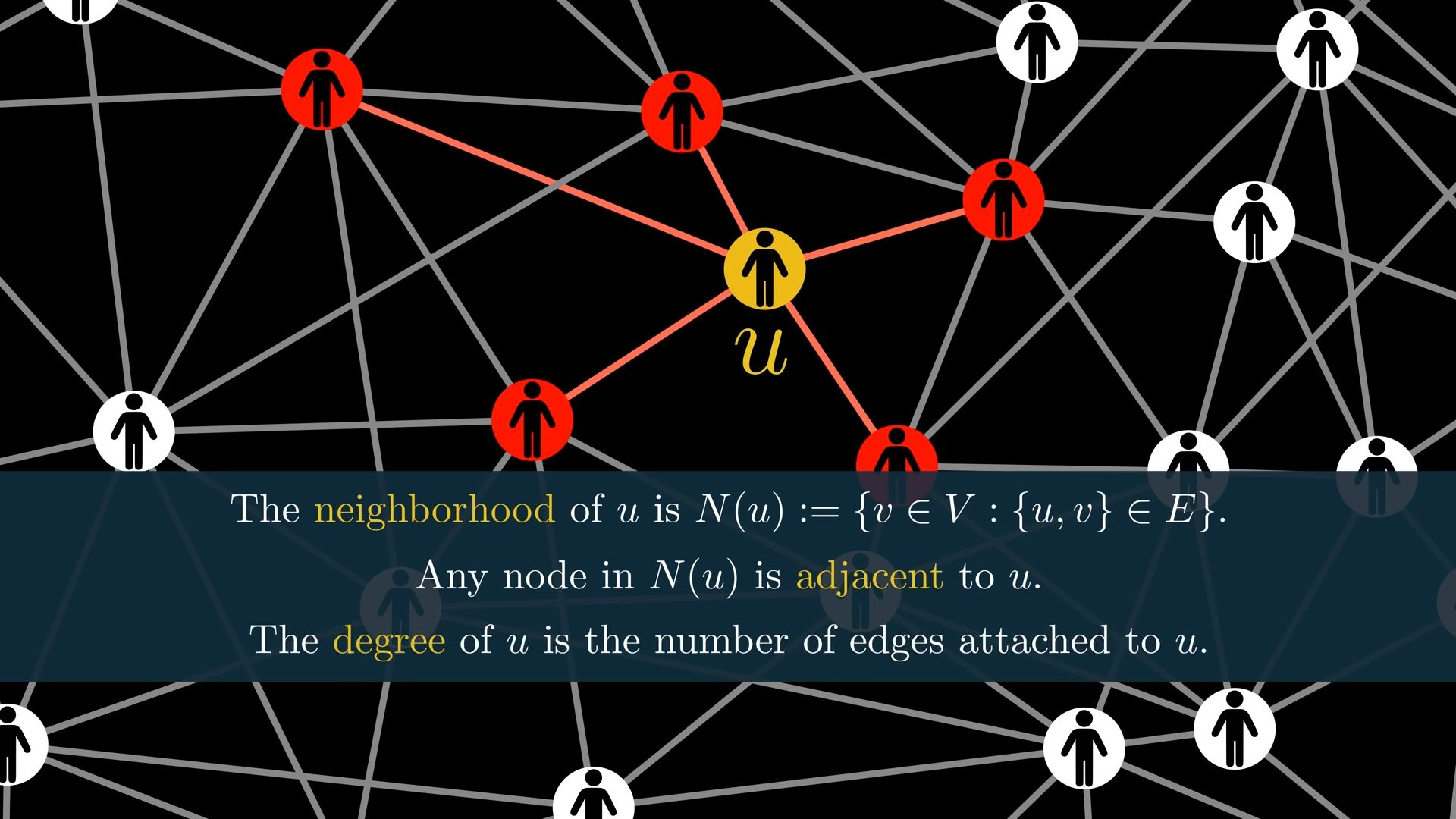
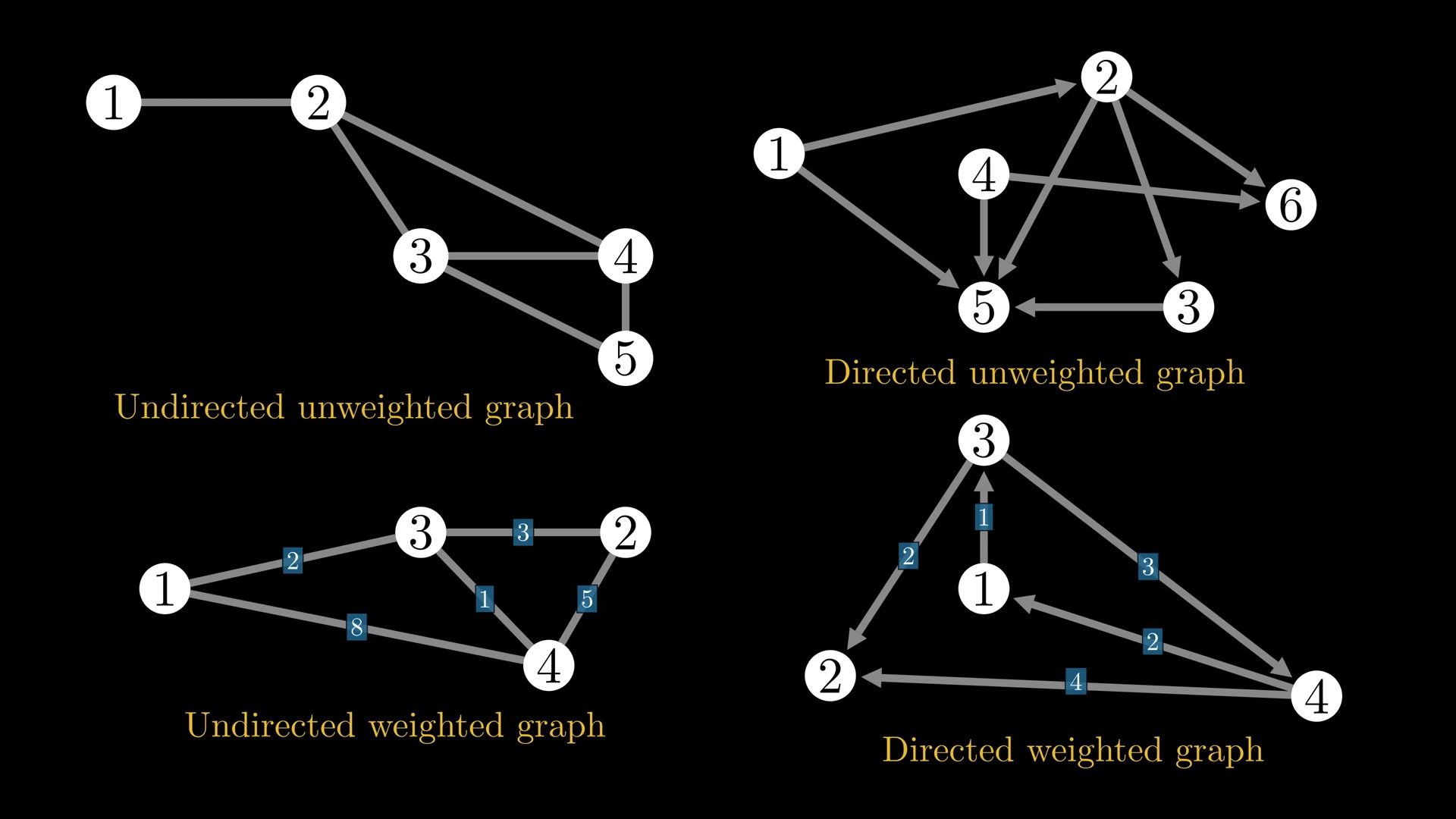
but important the degree of a node doesn’t always represent the number of neighbors of a Noe this is only the case if there isn’t more than one Edge between two nodes
04:02

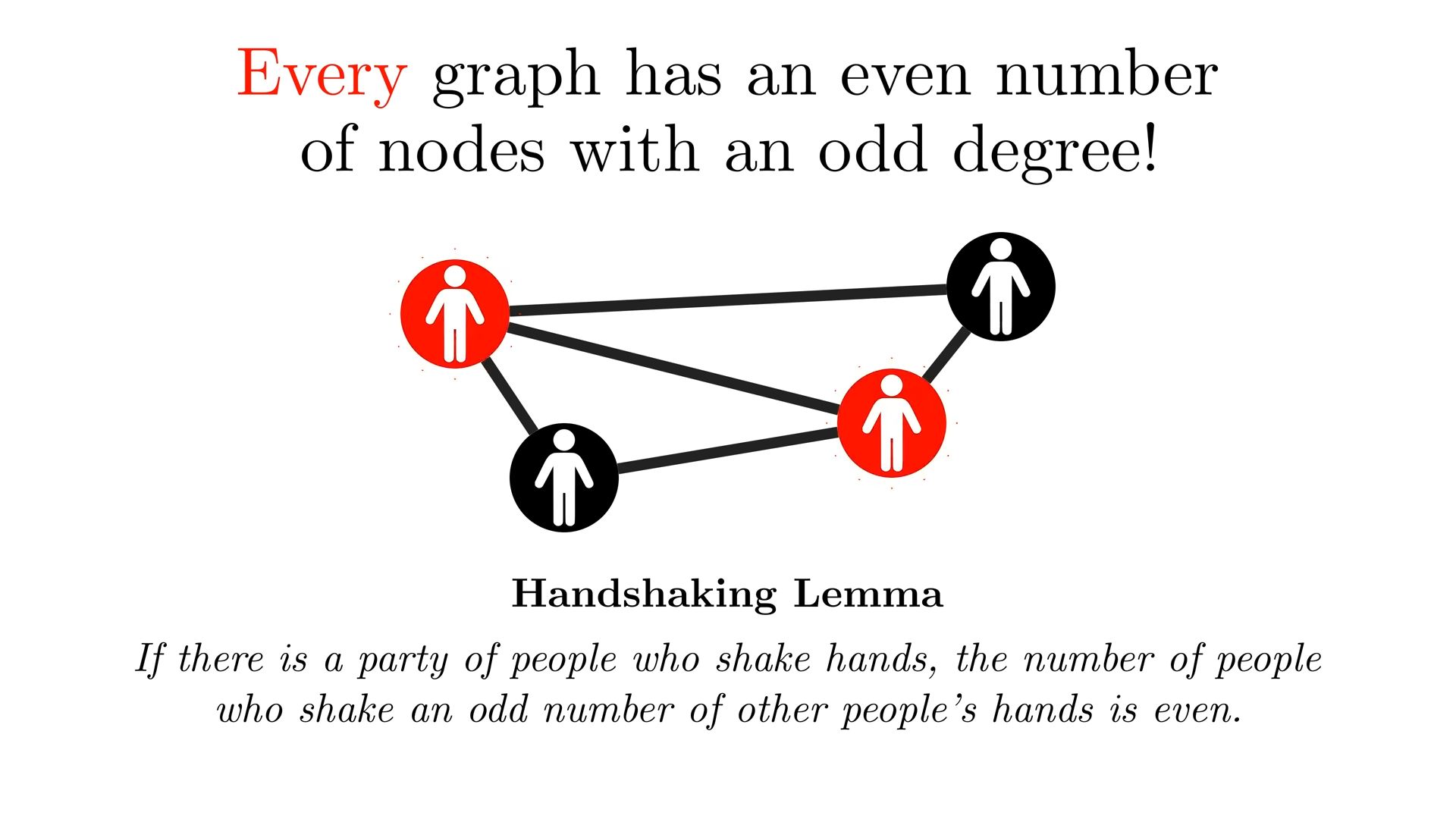
Sum of degrees of all nodes is ALWAYS EVEN
04:36

this graph is complete graph (every node is connected to all other nodes except itself.) has 57 nodes.
Hence every node is connected to (57-1=)56 other nodes. Sum of all degrees is 57x56 = 3192.
04:47
the total number of edges in this graph is given by half this number because by summing up all degrees one counts every single edge twice this lets us to suspect that the sum of all degrees in the graph is always equal to twice the number of edges in the graph.
The formula:
05:48
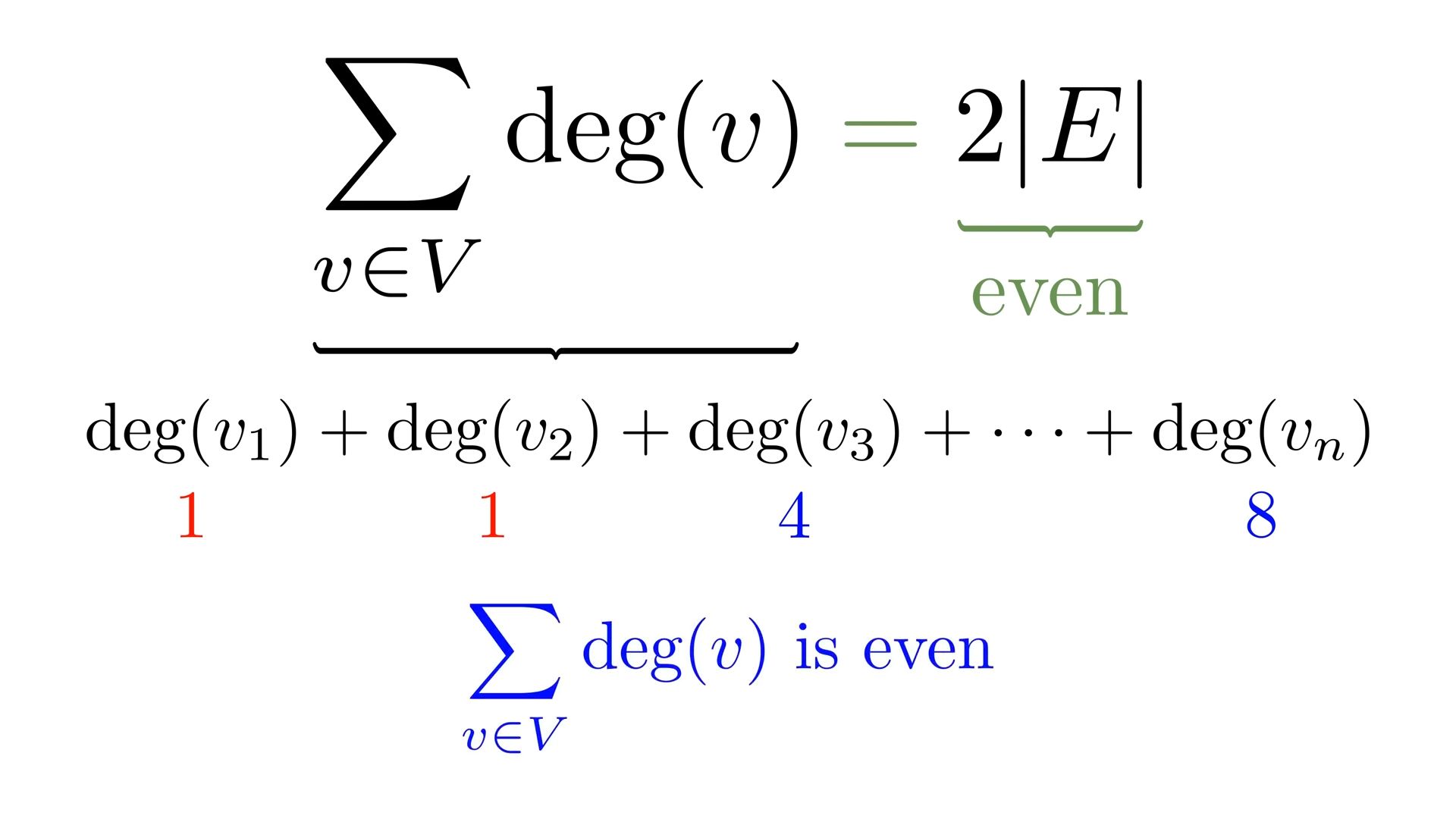
05:57
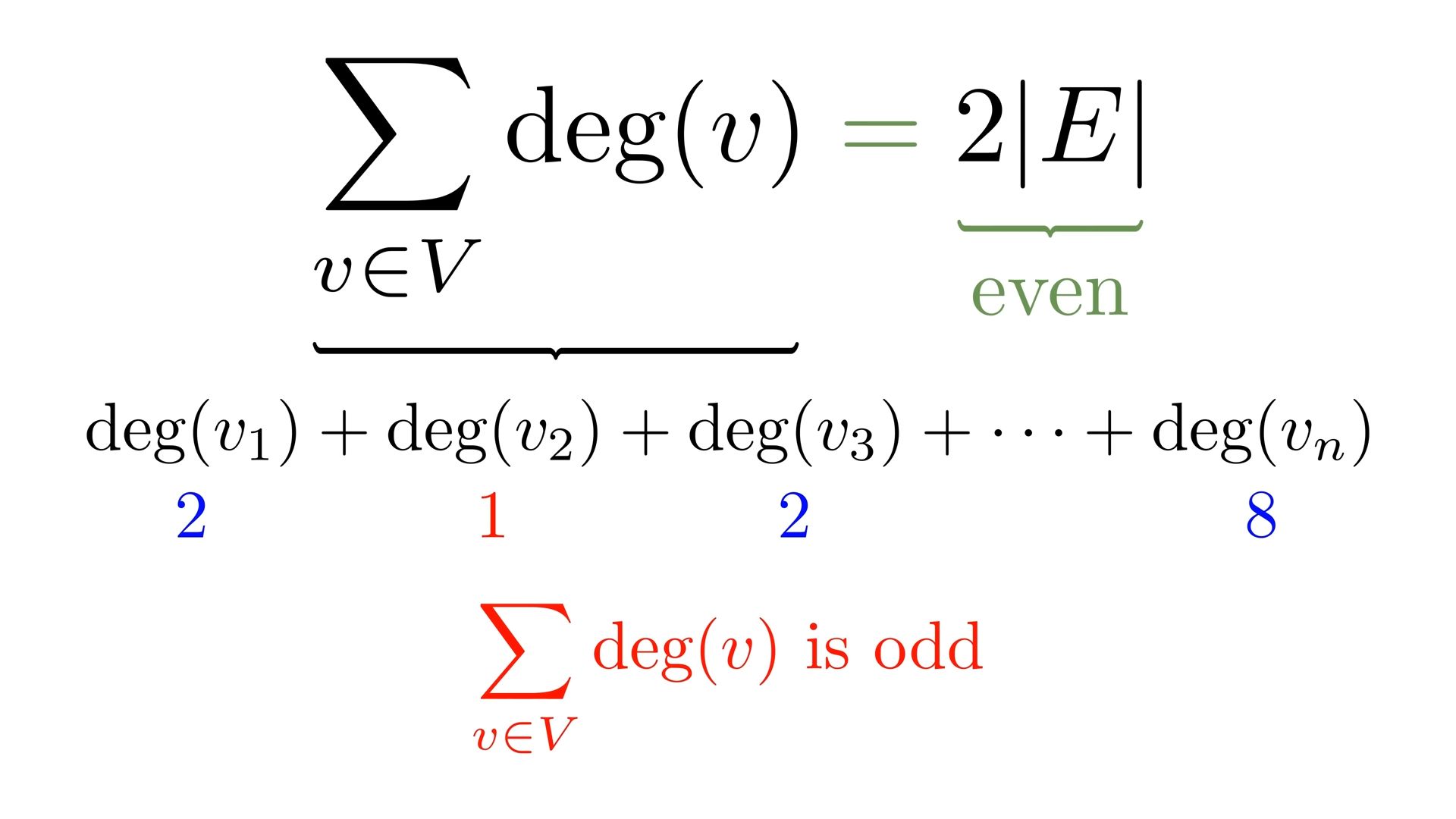
05:50
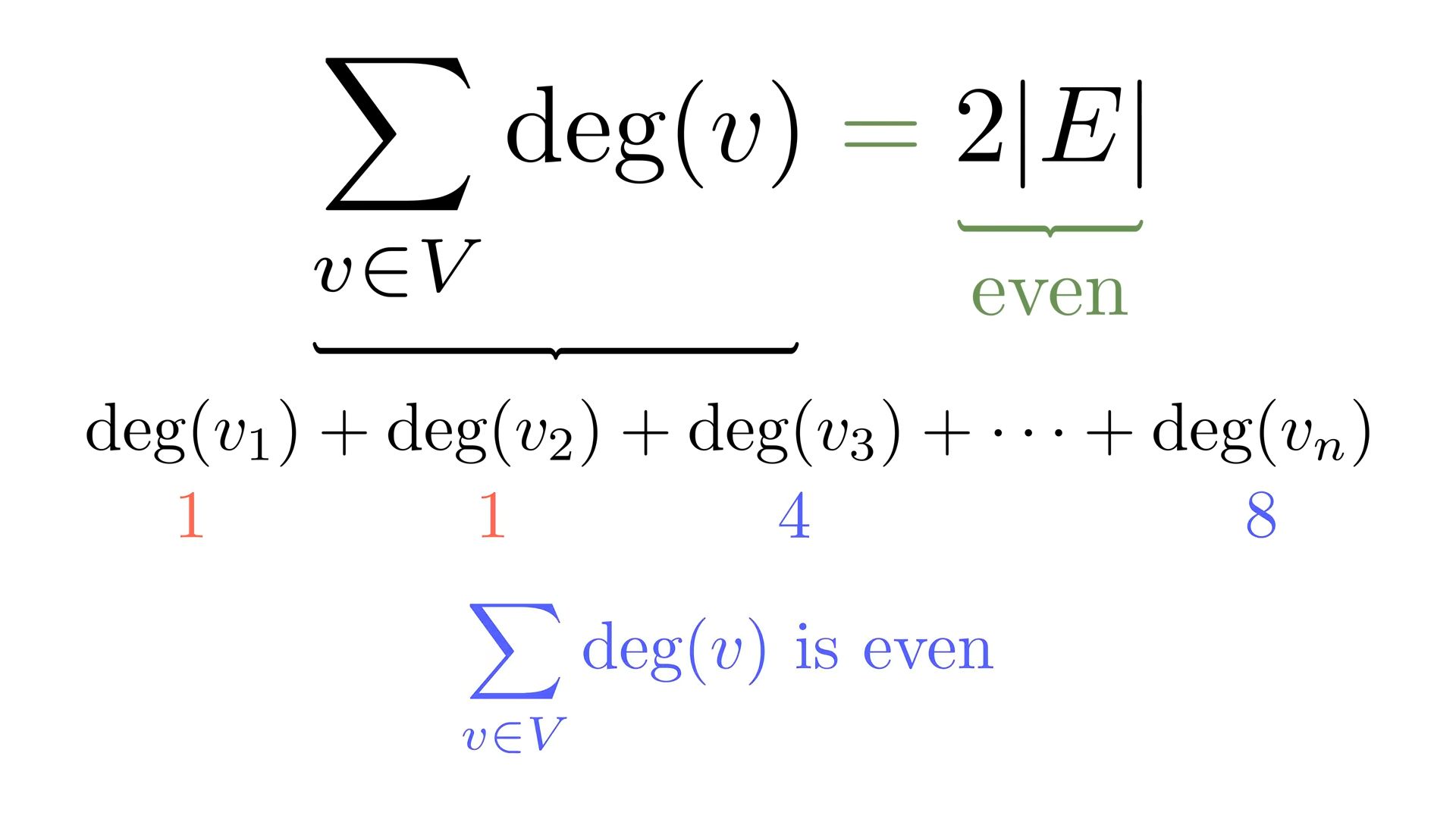
06:13
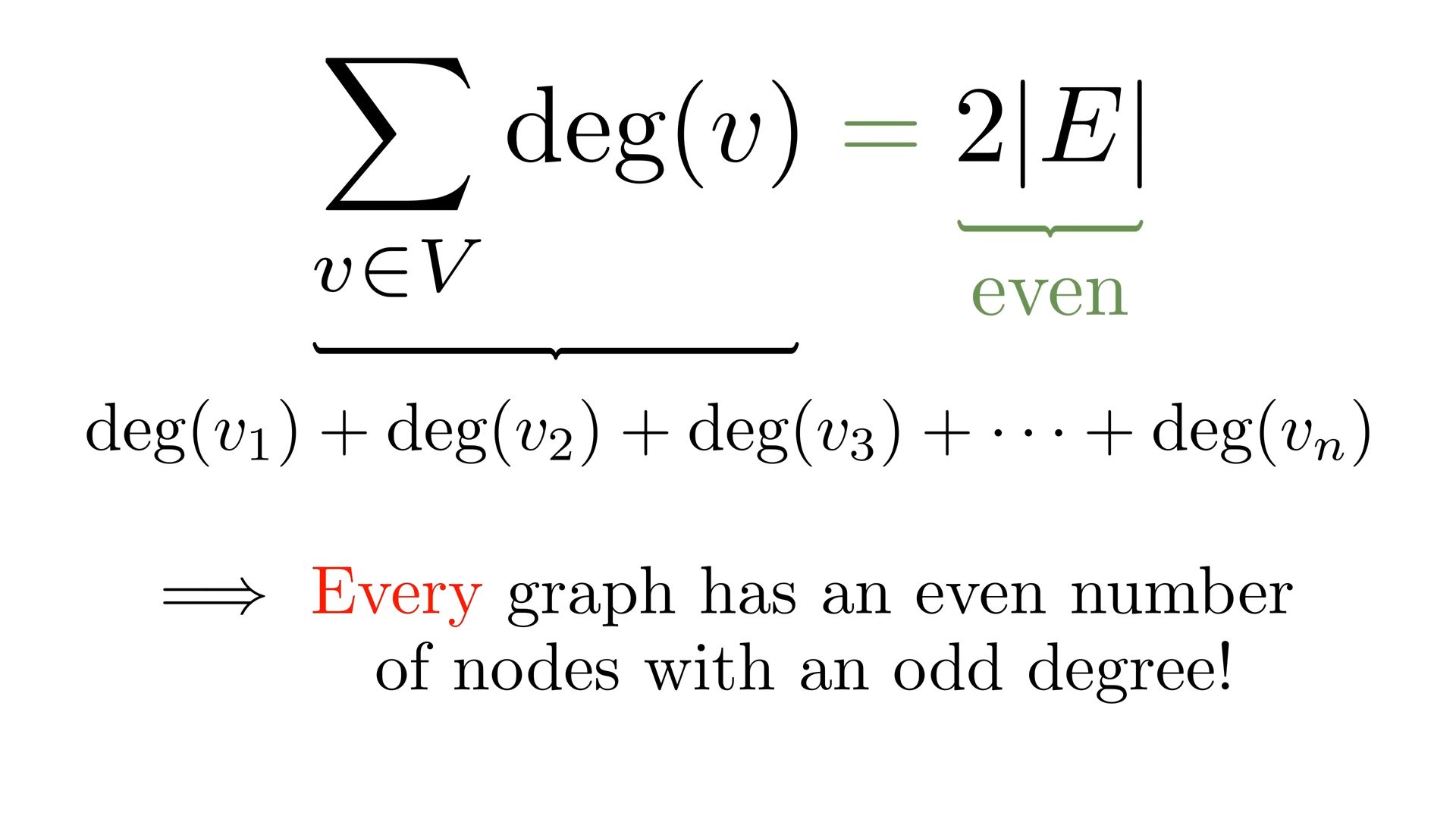
Corollary:
06:23
Graph Traversal#
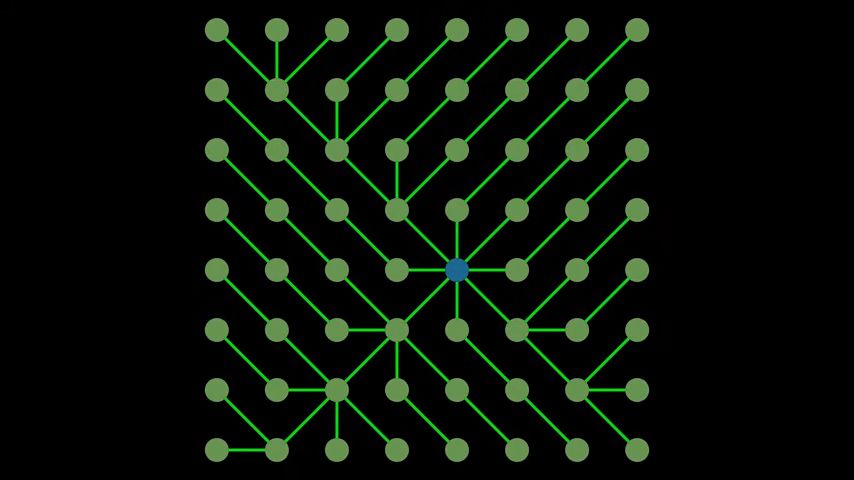
BFS - starts at a node and visits all its it’s neighbors. Layer by layer exploration of graph.
07:15

The subgraph generated by this algorithm is known as BFS tree:
07:32
07:16
the subgraph generated by this algorithm is known as a bfs tree which offers valuable information about the underlying graph:
for instance shortest paths from the starting nodes to all other nodes
if the length of a path is characterized by the number of its edges.
DFS - the algorithm follows the approach to explore the graph in depth first. It selects in every iteration a neighbor node possibly a random neighbor as the next node and continues in this way until it gets stuck then the natural way out think about a maze is to backtrack to the last note with unvisited notes in its neighborhood.
08:16

08:20
The resulting subgraph the DFS Tree looks a bit familiar to a maze and indeed with the right modifications this simple algorithm can also be used to generate a maze.
Creating Maze using DFS
09:17

09:44

09:31
Note that through the application of DFS this maze has a solution. Since DFS 09:33calculates a path from the starting nodes to all notes in the graph. In other words there is a path from the starting notes to any other nodes here.
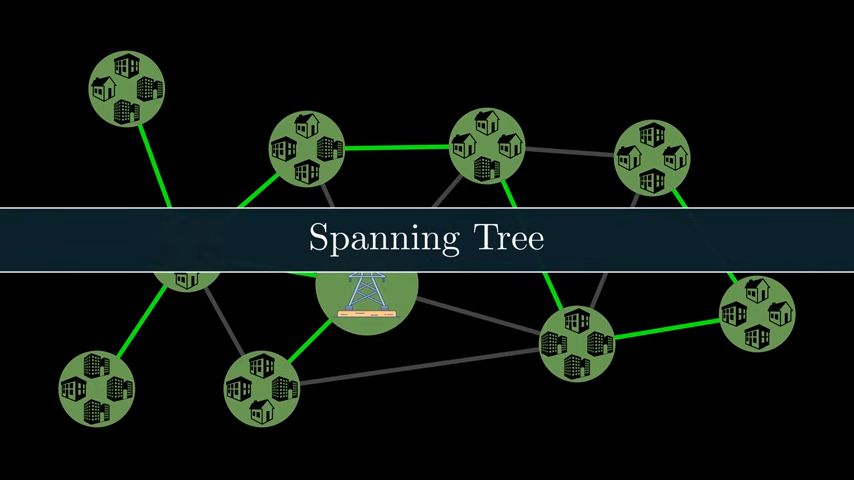
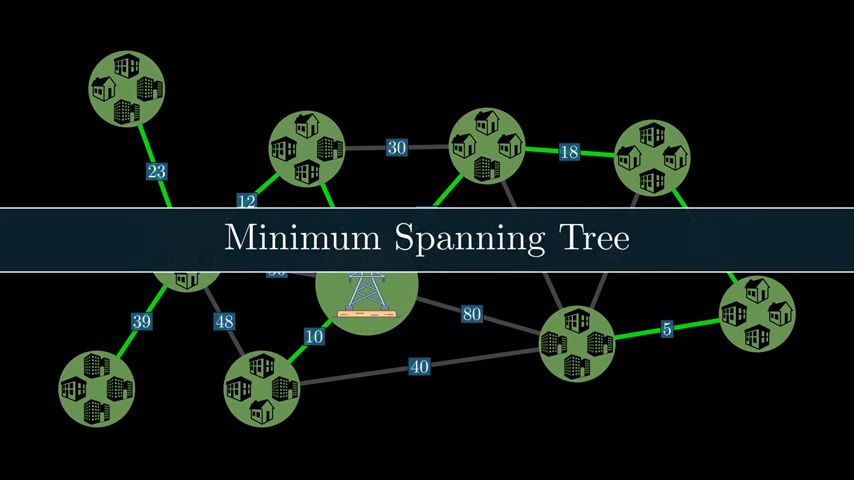
Example: Electricity Wire distribution in city
10:25
10:49
10:39
the distribution of wires such that every town gets access to electricity therefore one would search for a minimum spending tree in the given graph which is a spanning tree with the least possible total cost.
Shortest Path Algorithms#
10:43
Very important in graph Theory especially in the era of navigation systems like Google Map maps are shortest path algorithms. Think about a map of country where each note represents a city and the edges are labeled with costs such as the kilometer distances between two nodes or the duration to travel between two adjacent nodes.

The Origin of Graph Theory#
12:42
The citizens decided to create a game for themselves. Their goal being to devise a way which they could walk around the city crossing each of the Seven Bridges in Koenigsberg exactly once.

Seven Bridges in Koenigsberg#
Walk#

Definitions
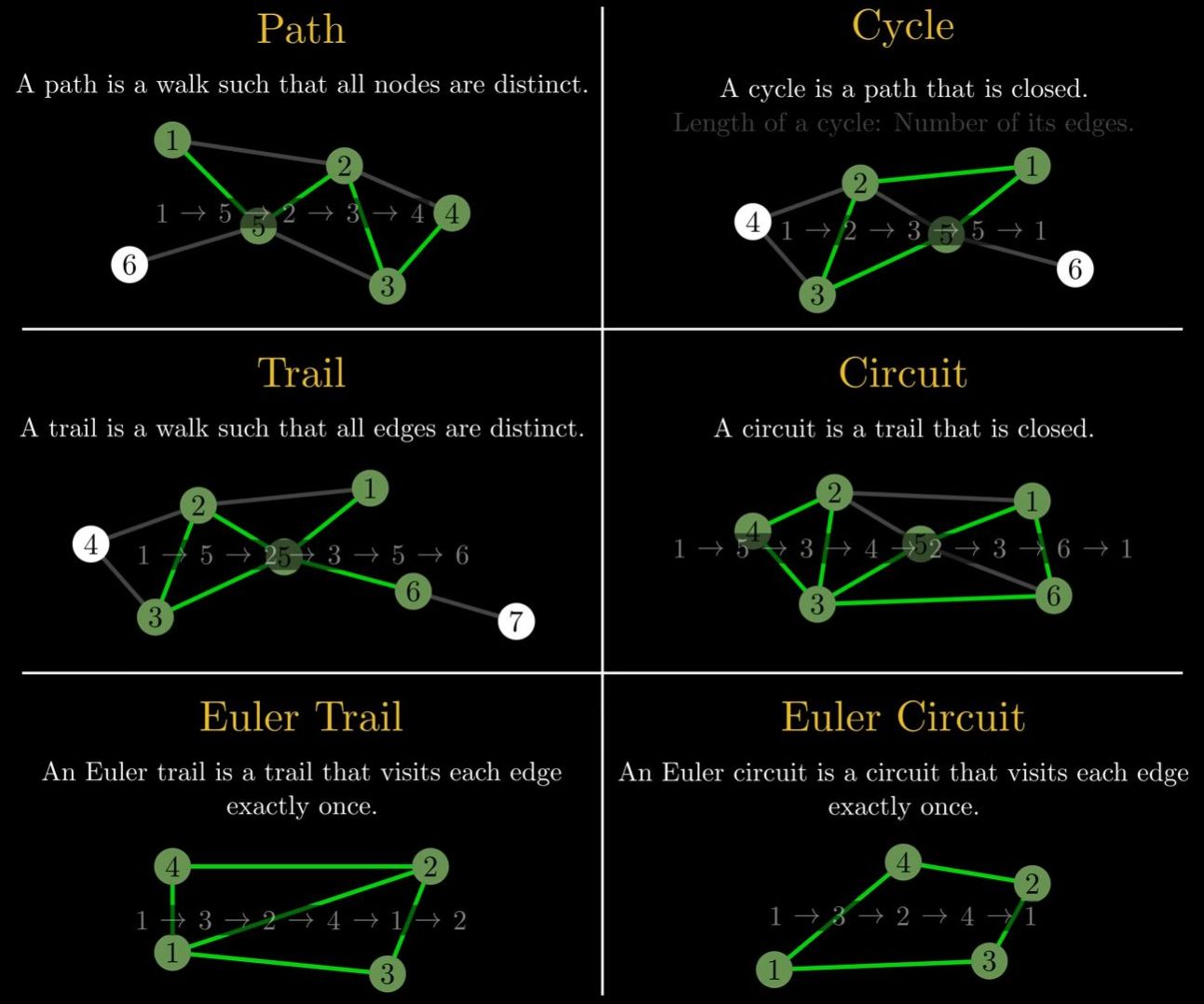
Path#
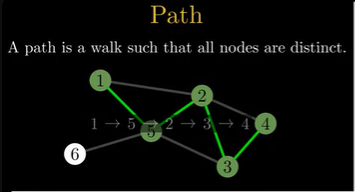
A path is a walk in a graph such that all visited nodes in the walk are distinct. So in the general definition of a path, it is not allowed to use nodes more than once.
Cycle#
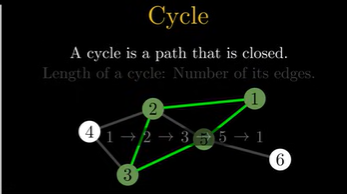
A cycle is a path that is closed meaning it starts and stops at the same at the same nodes. Furthermore, the length of a cycle is given by the number of used edges in cycle.
Trail#
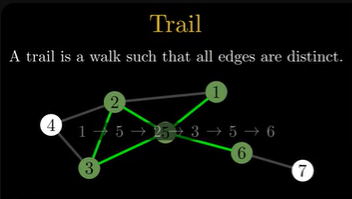
A trail is a walk such that all used edges are distinct. Furthermore, it can visit notes more than once.
Circuit#
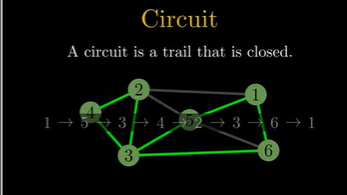
A circuit (not to confuse with a cycle important) is a closed trail.
Euler Trail#
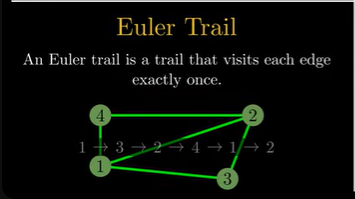
16:48
An Euler Trail is a trail that visits each Edge in the corresponding graph exactly once. (While such a trail is often referred to as an Euler path it basically isn’t a path because it can visit nodes more than once.)
Euler Circuit#
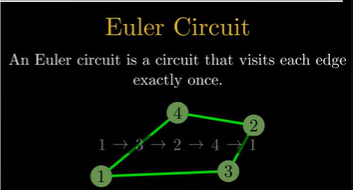
17:24
An Euler Circuit is a circuit that visits each Edge in the graph exactly once.
18:00
17:36
One can observe immediately is that the graph in the bottom right corner here which contains an Euler circuit has only nodes with an even degree. And in fact, a graph that contains at least one note with an odd degree cannot have an Euler circuit.
Explanation:
Due to odd degree you wont be able to return to this node anymore (if started here) as required by Euler Circuit.
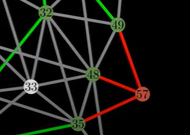
Or even if started from even degree node, we will get stuck in odd degree node as we cannot leave it.
Euler’s Theorems#
Assertions:
19:19

Graph Data Structures#
20:42
21:14
21:06
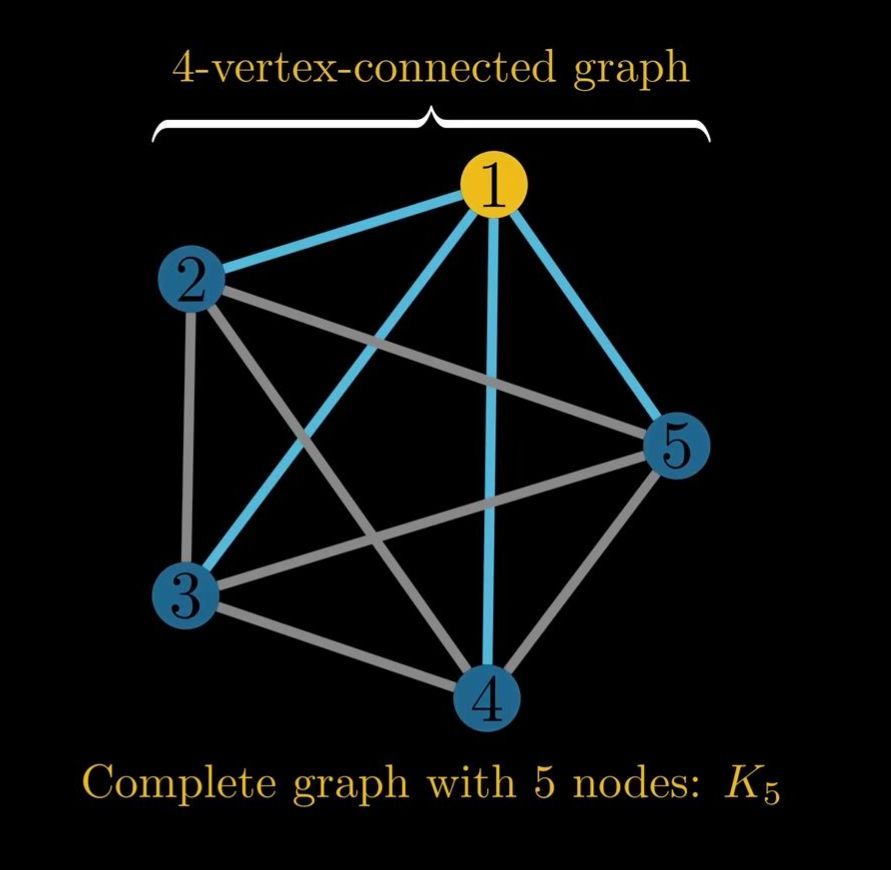
A graph G is set to be K vertex connected if it contains at least K+1 vertices but does not contain a set of K-1 vertices whose removal disconnects the graph.
22:13
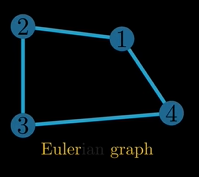
Another important graph is for example the oiler graph which is a graph where every node has an even degree ensuring the existence of an Euler circuit.
22:42
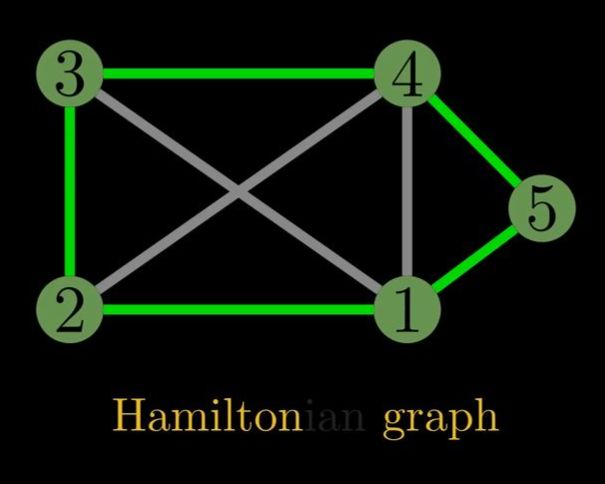
Hamilton graph which is a graph that contains a Hamiltonian cycle a cycle that visits each note exactly once.
22:39
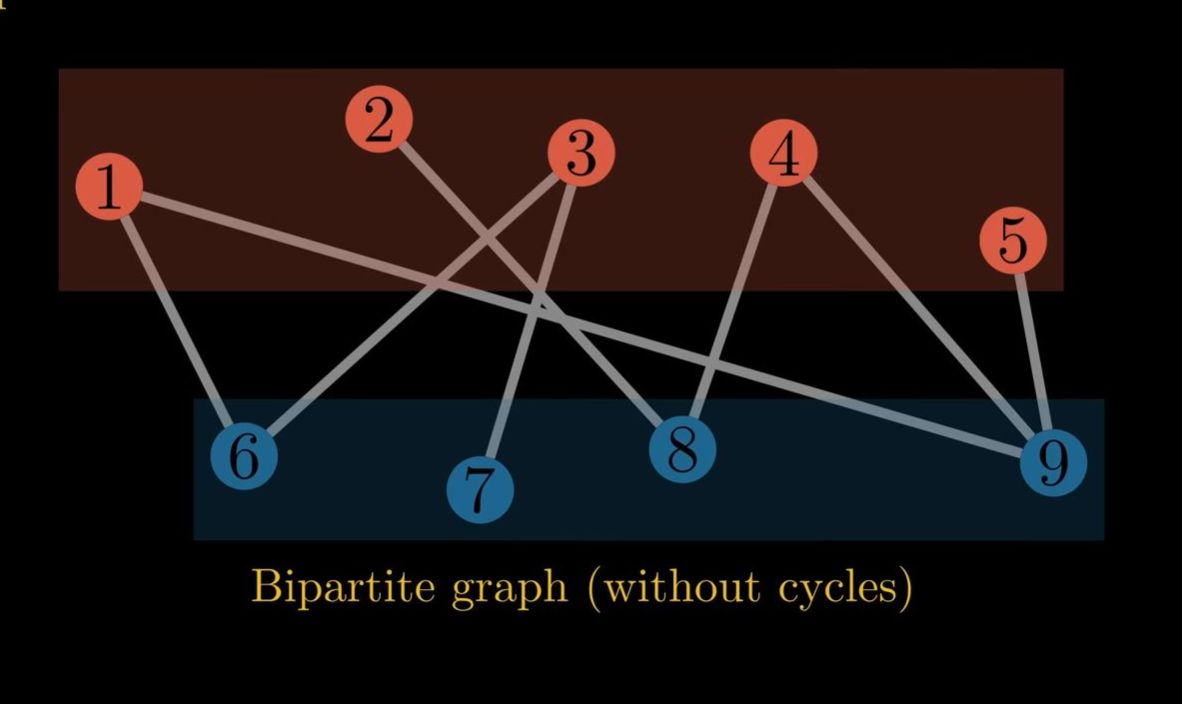
A bipartite graph is defined as a graph whose notes can be divided into two disjoint sets in such a way that no two nodes within the same set are adjacent in this graph.
Notes this is a bipartite graph without Cycles
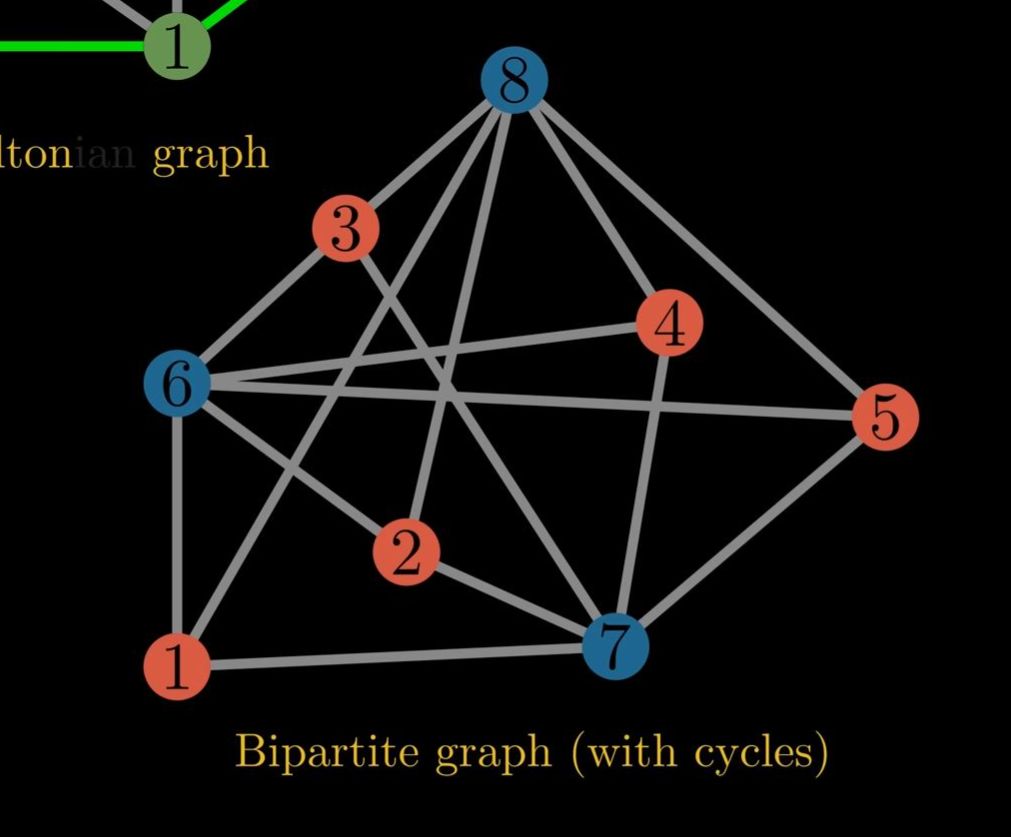
A graph with Cycles can also be Bi-Partite.
Furthermore, a graph is in general bipartite if and only if every cycle is even. This means that every cycle in the corresponding graph has to consist of an even number of edges.
Forests#
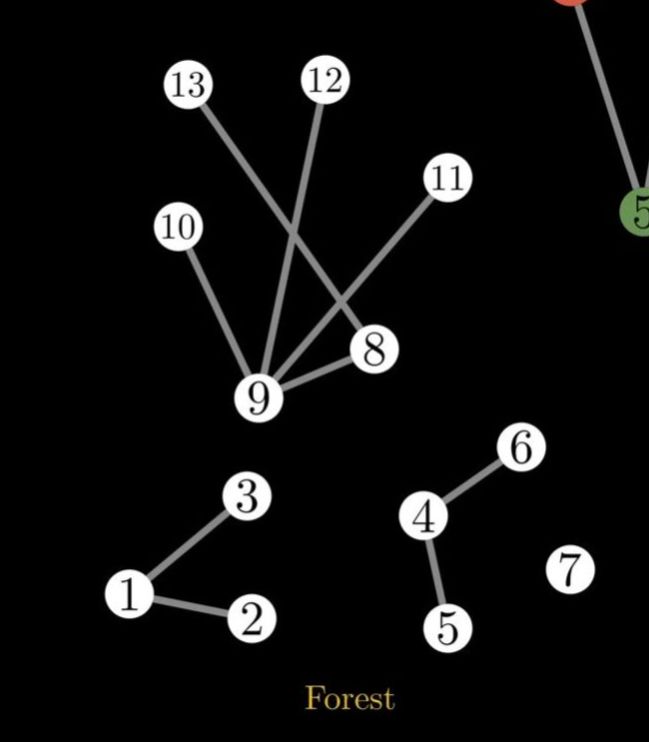
A forest describes a collection of trees. Trees are graphs that have always the minimum number of edges necessary for connectivity. A tree will be typically Illustrated with a structure like this.
Binary Trees#
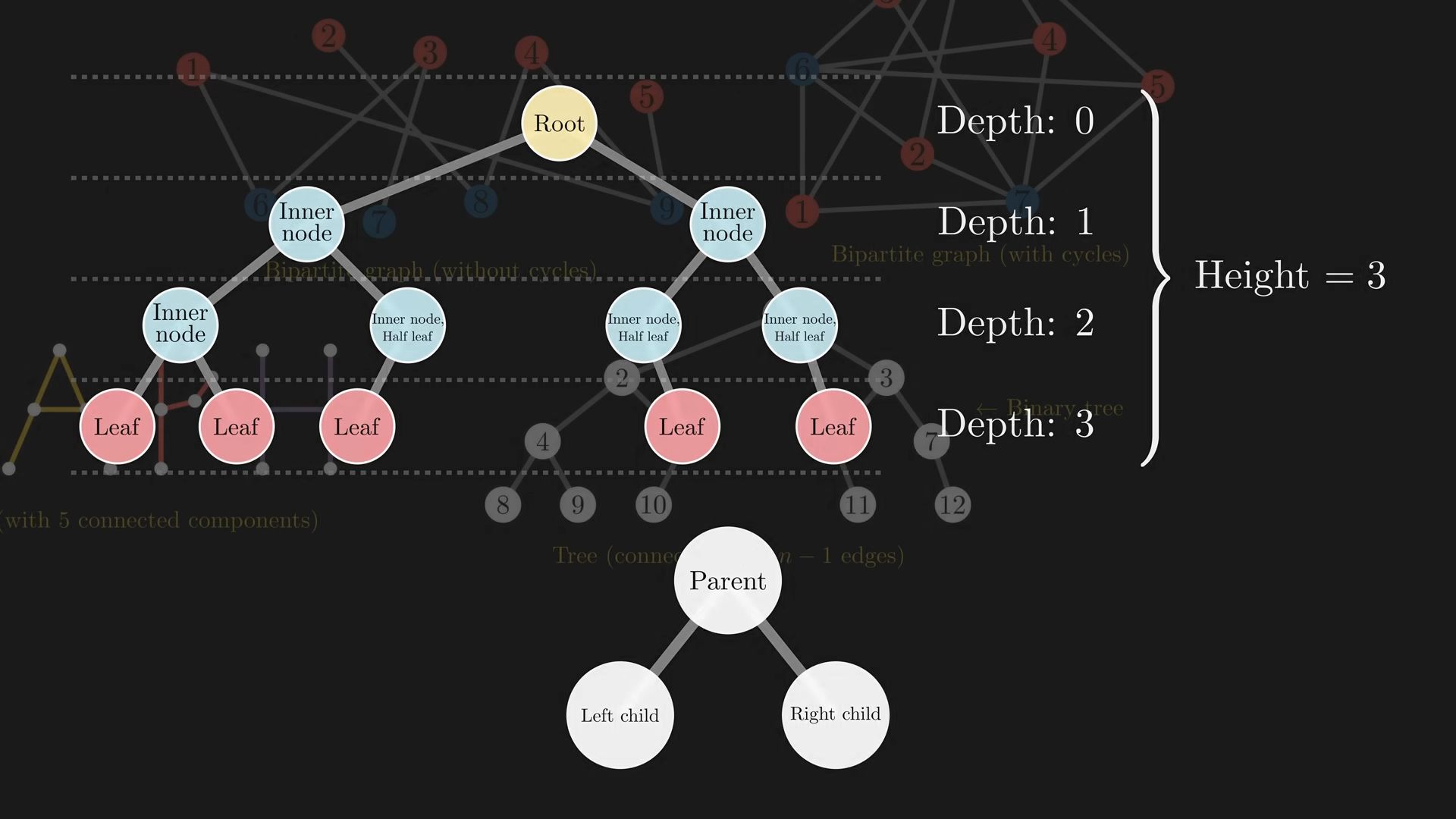
Specifically, this here is a binary (Each node has at most 2 children).
25:34
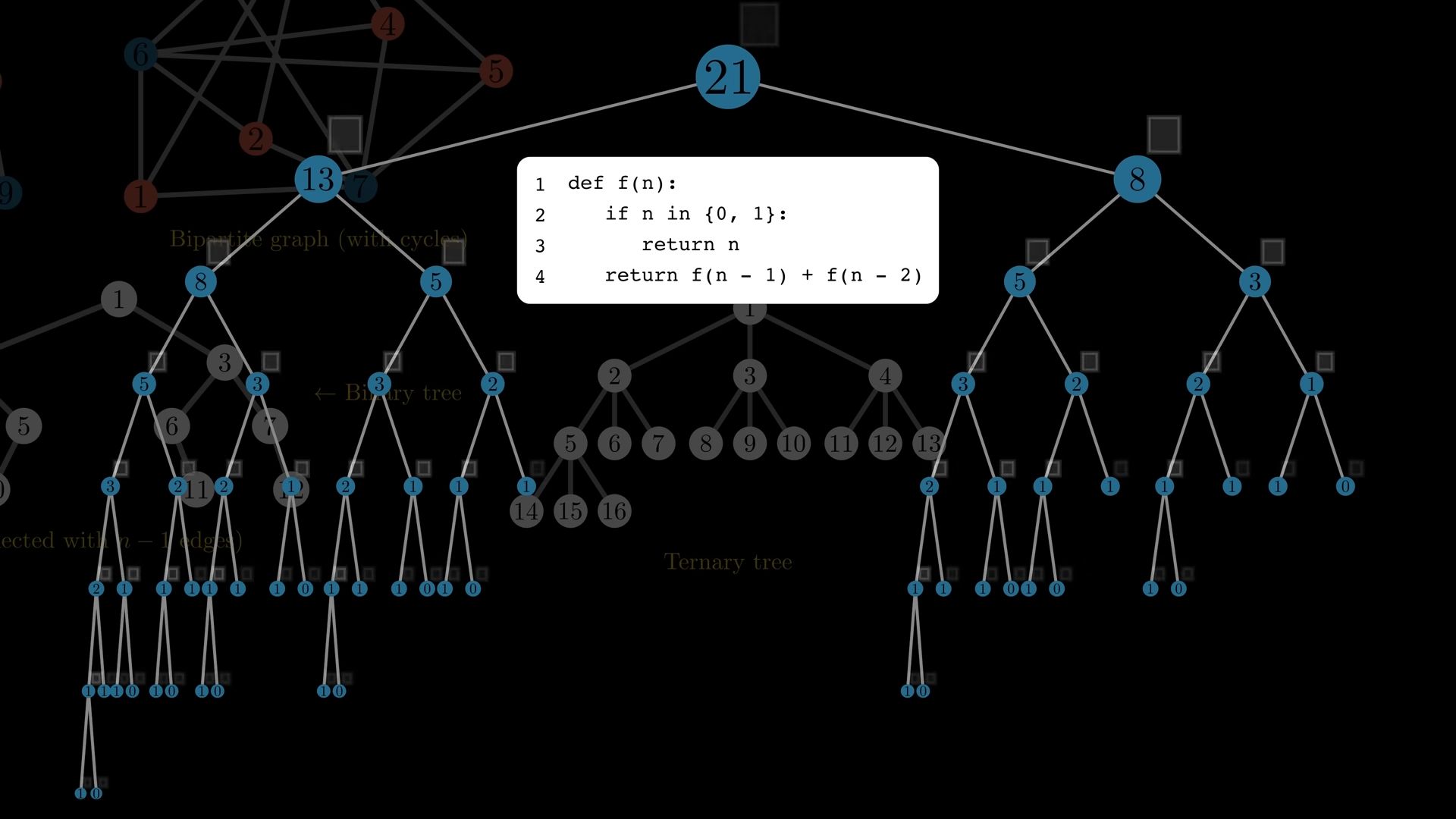
Binary trees are used in various applications for instance to visualize the execution of many recursive algorithms here for example of the execution of a recursive function that calculates the eight Fibonacci number.
26:09
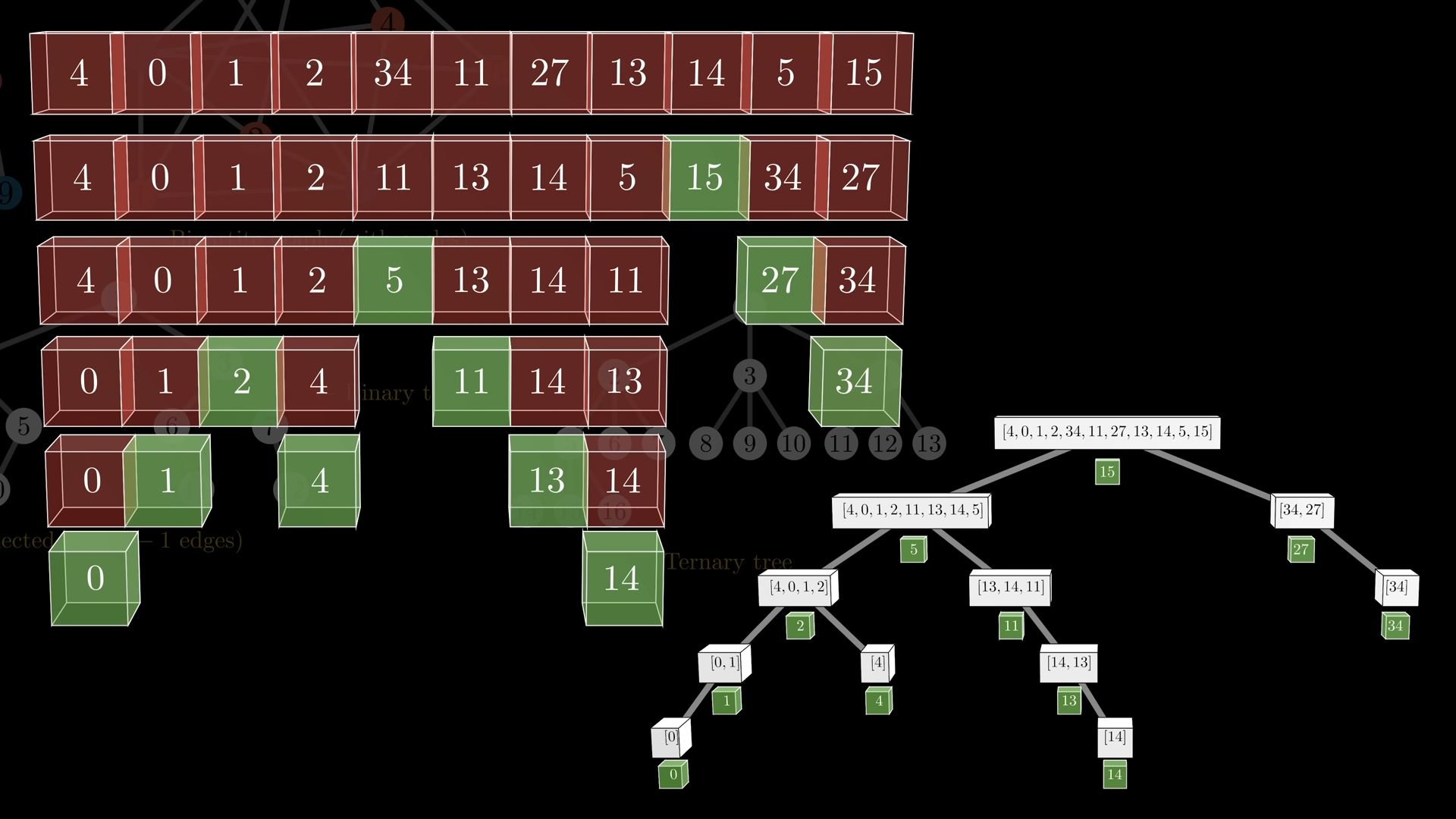
Quicksort
Types of Binary Tree#
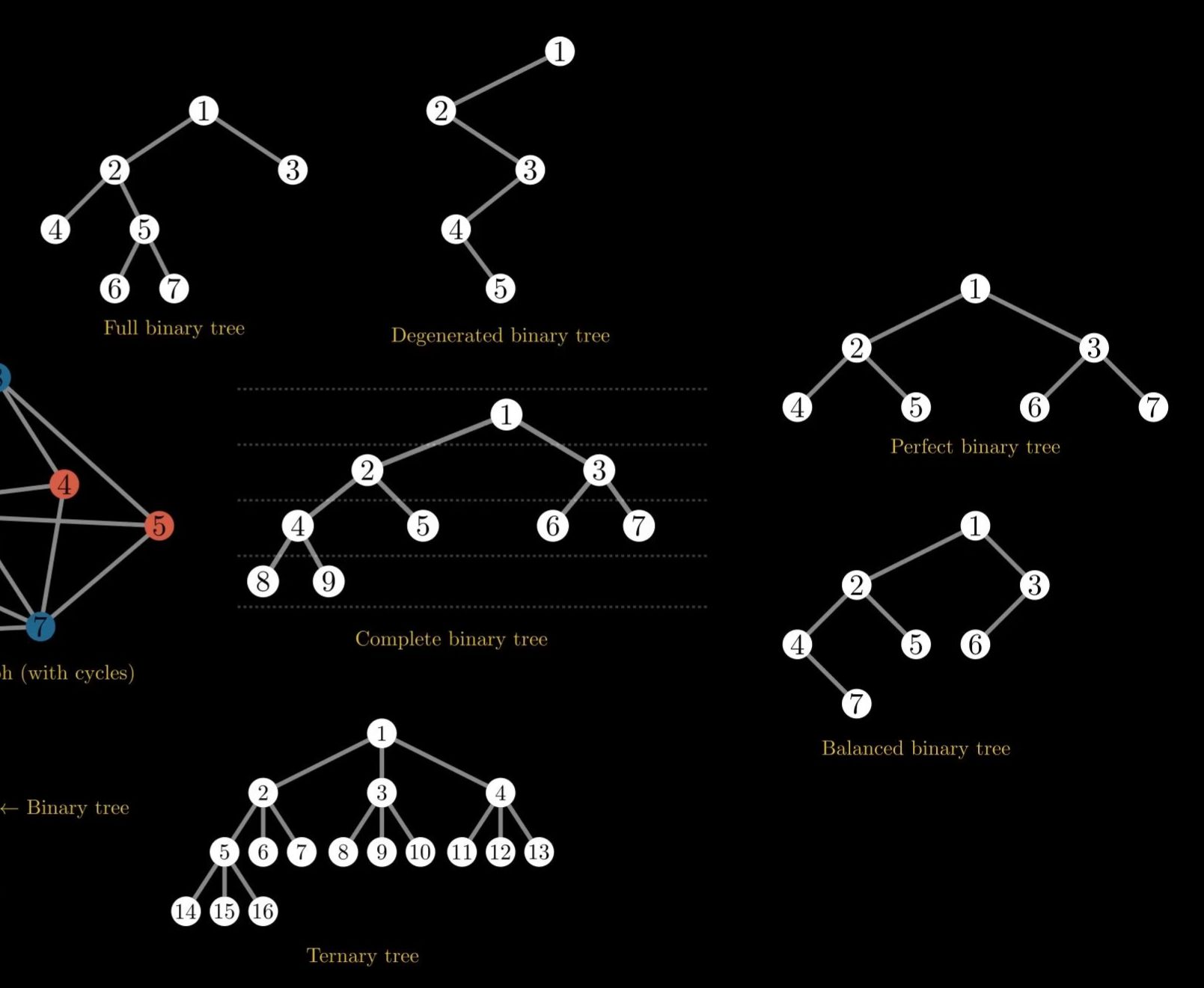
The complete binary tree is characterized by the property that it must be completely filled on every layer of the graph except for the bottom layer and all nodes must be as far left as possible.
In a full binary tree, every node has either zero or two children but never just one child. But if a binary tree has only one child per parent either a left or a right child and this through the entire tree then it is called a degenerated binary tree.
The perfect binary tree is characterized by the property that every layer is completely filled with all leaf nodes on the same layer.
Basic Data Structures#
27:55
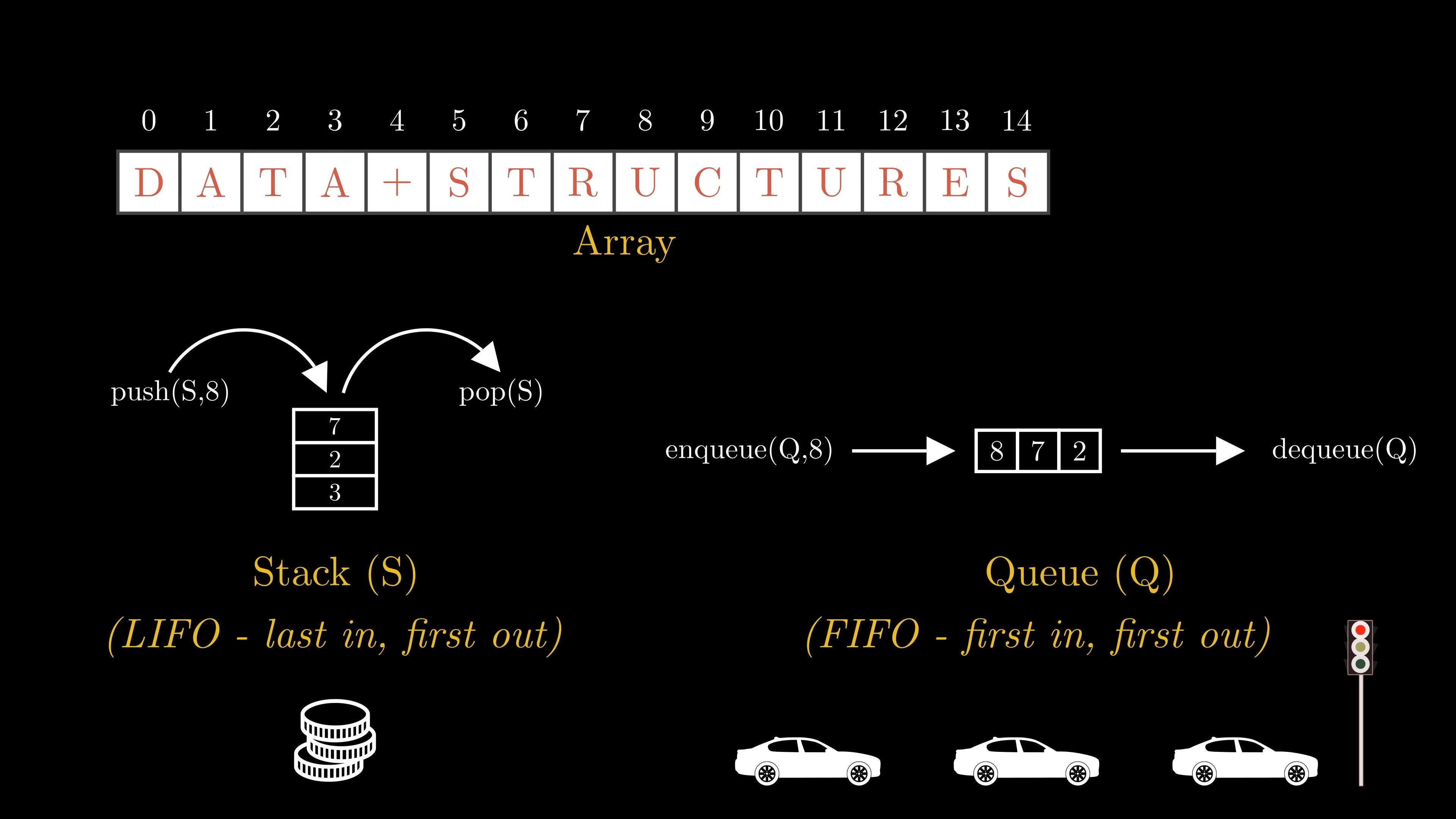
30:06

31:44
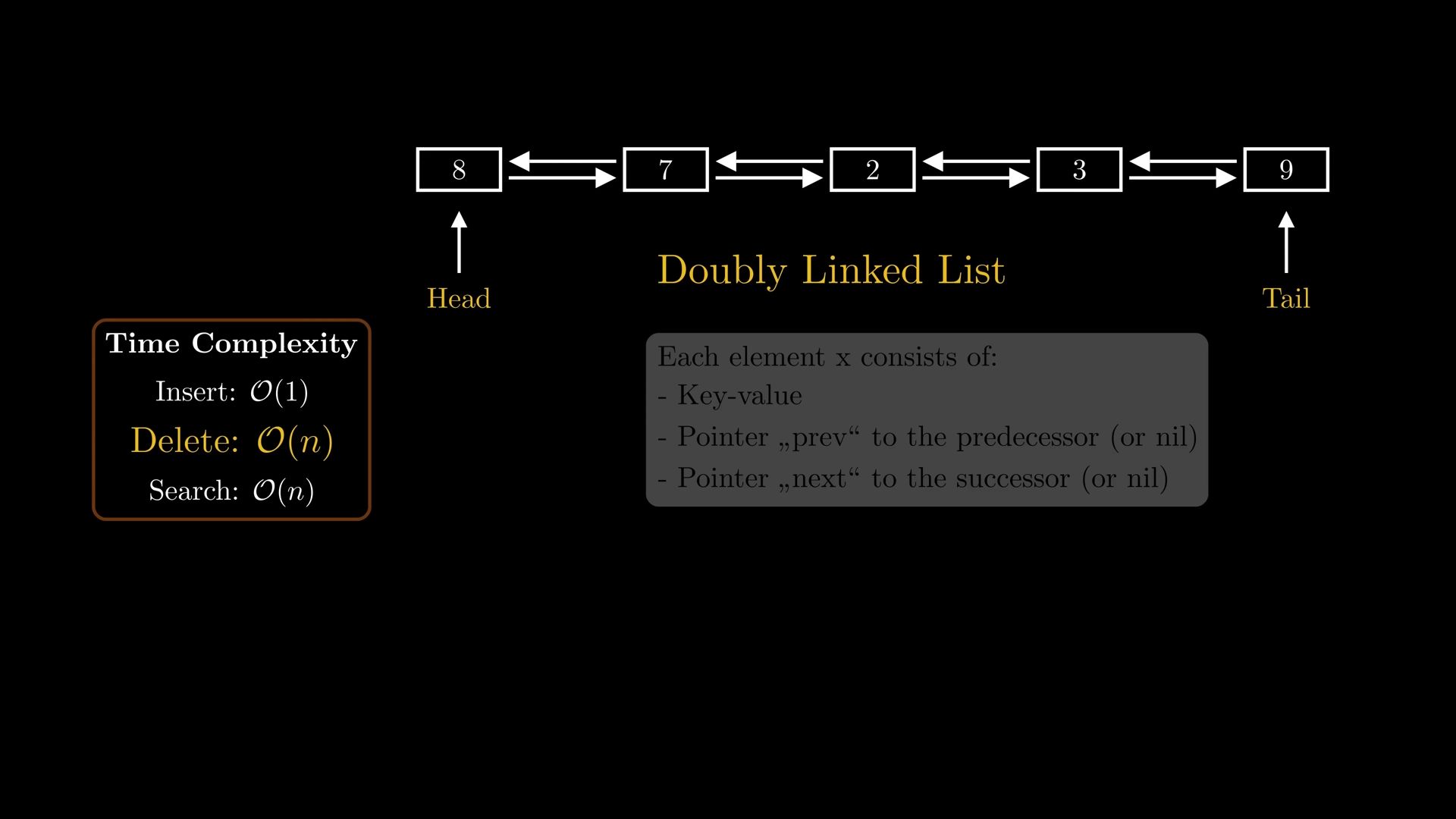
30:50
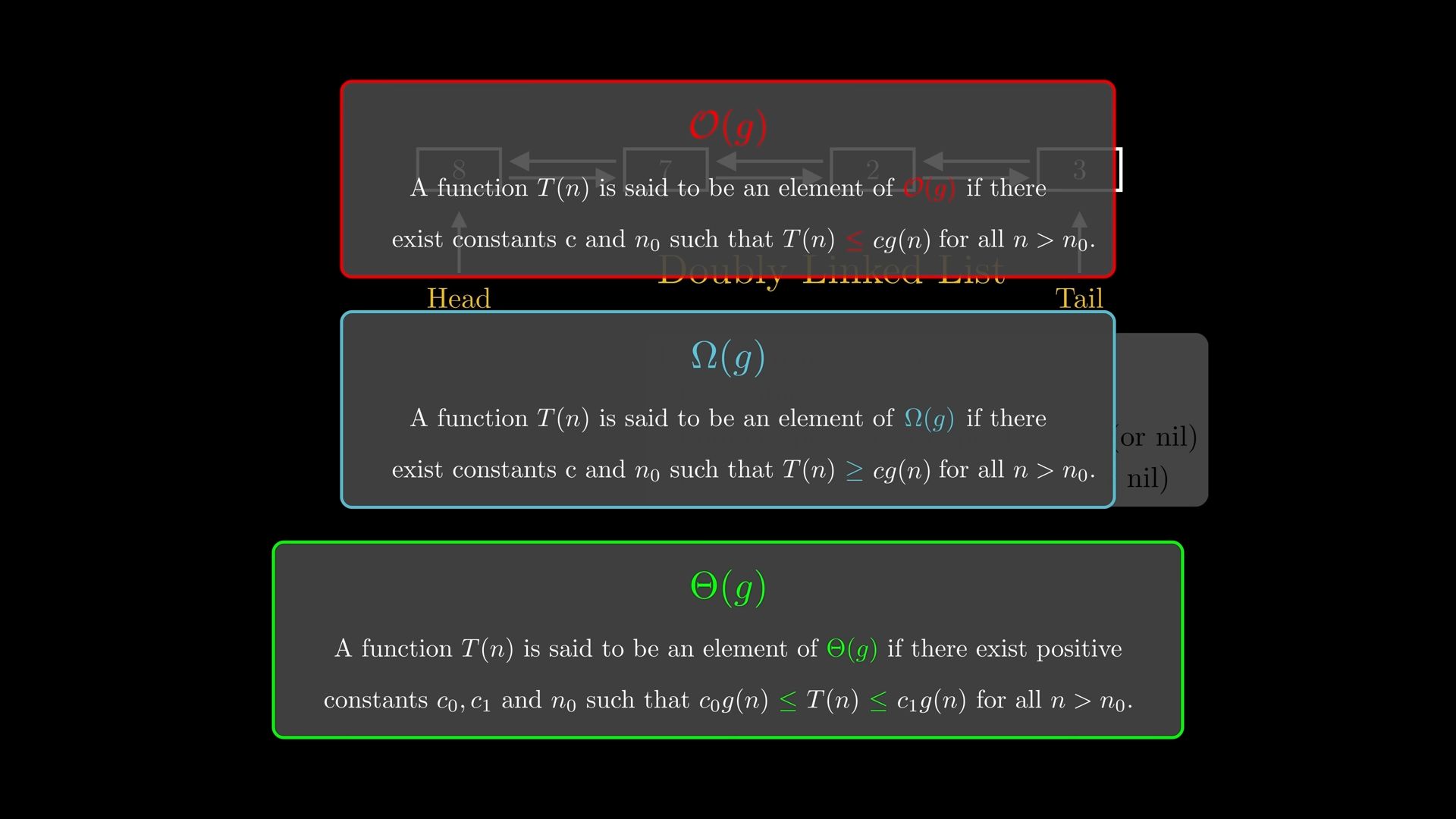
32:41
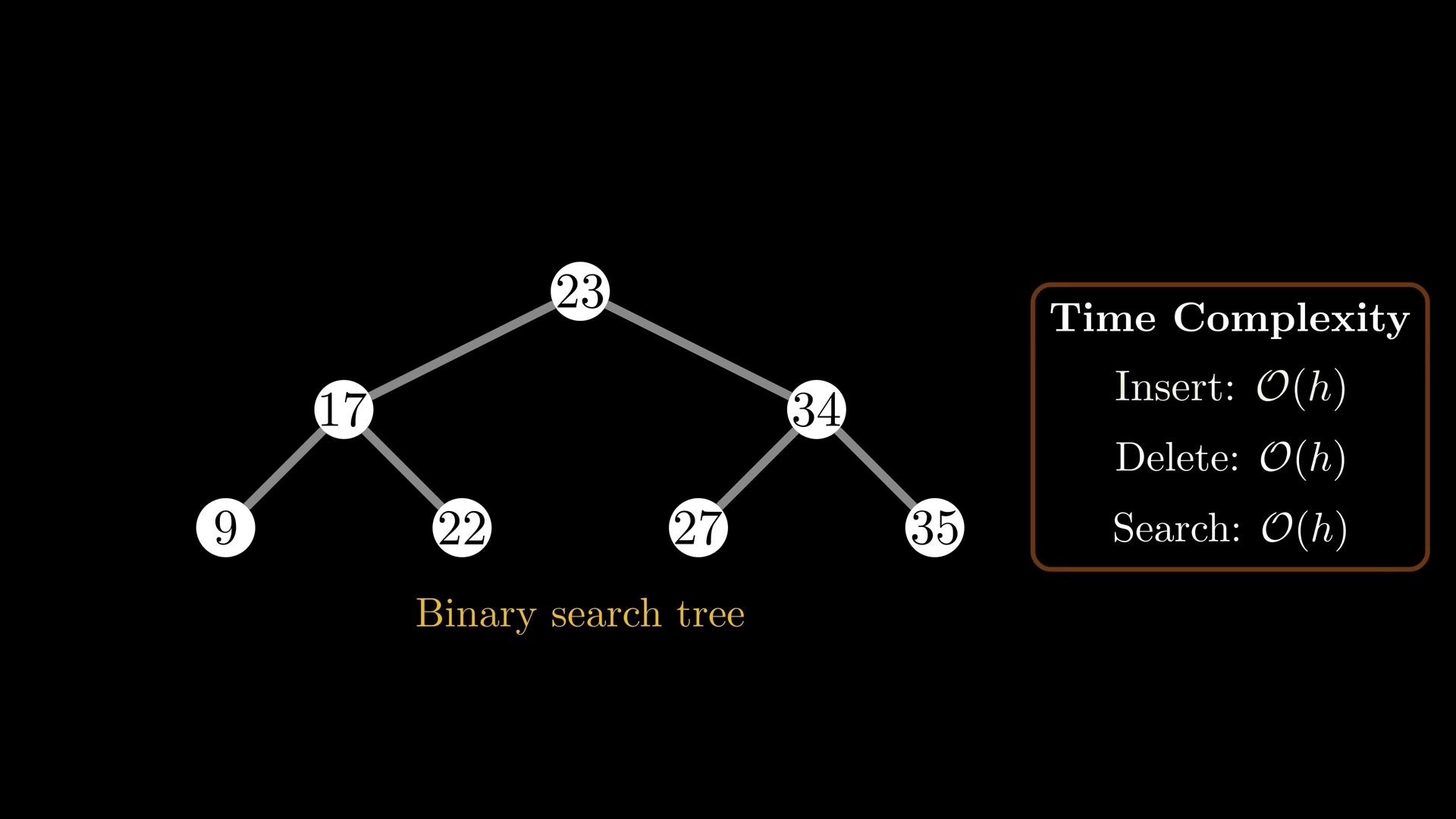
Binary search tree is a binary tree with the additional property that the key of a parent note is always larger than the key of its left child and smaller or equal to the key of its right child.
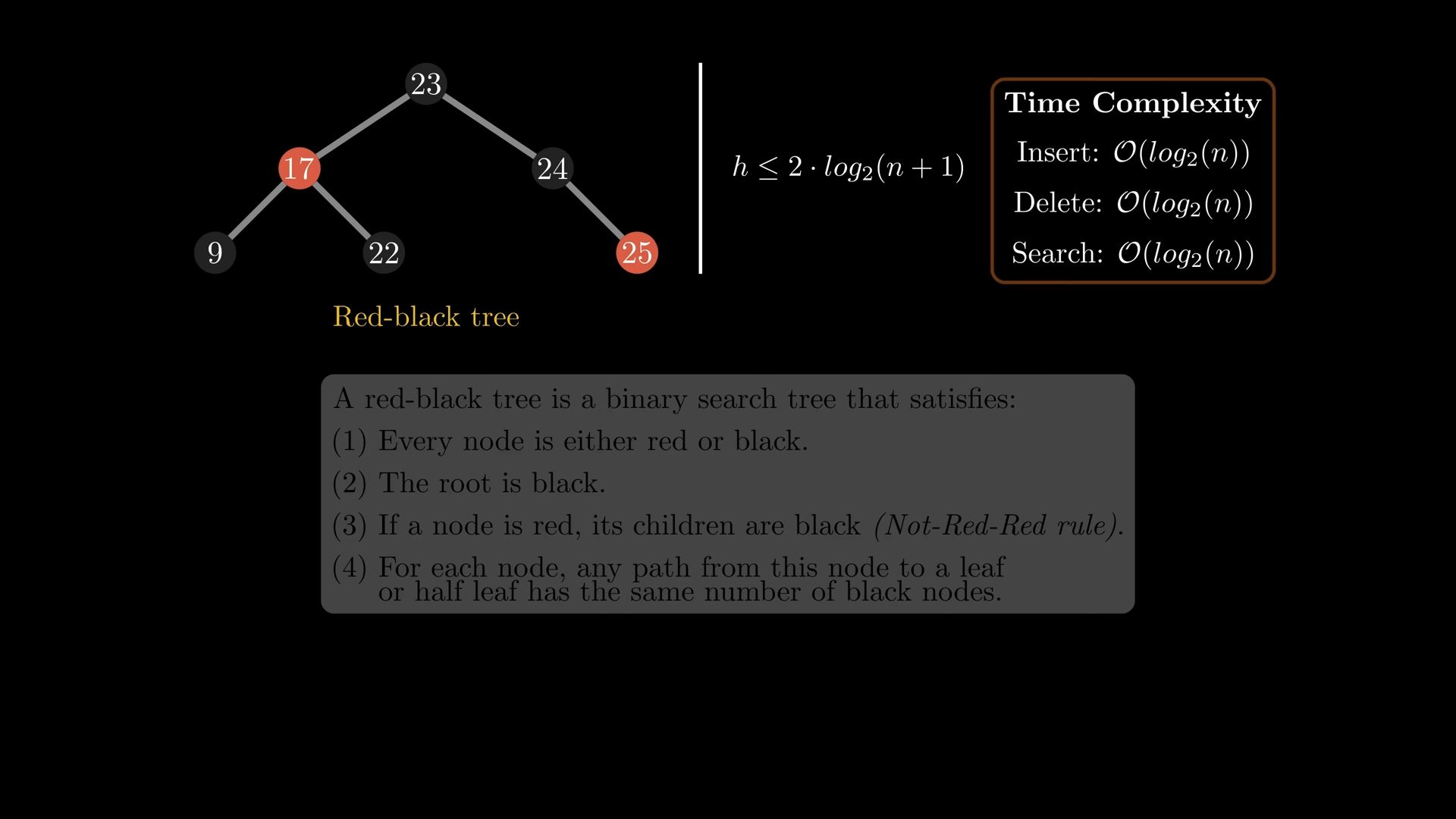
The red black tree guarantees a height that is smaller or equal to \(2.\log_2(n+1)\) where n denotes the number of notes in the tree such a tree satisfies the properties in the image.
38:26
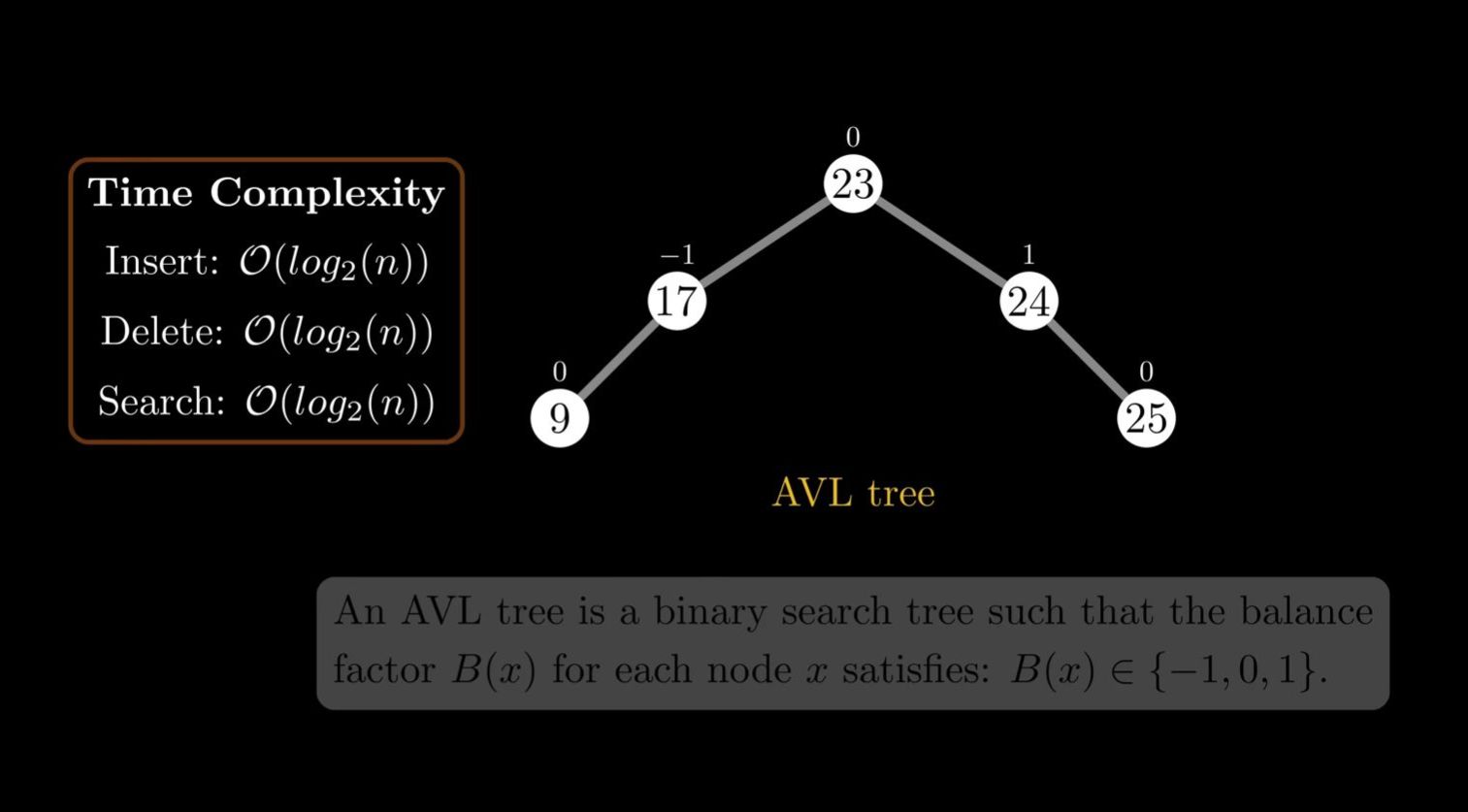
AVL trees are binary search trees where the heights of the two child sub trees of any parent nodes differ by at most one. The small indices over the notes in an AVL tree represent the balance factor indicating the height difference between the left and right sub tree of each node. This balancing prevents the tree from a degeneration to maintain efficient search insert and delete operations.
Heaps#
There are two kinds of heaps. Max heaps and mini heaps.
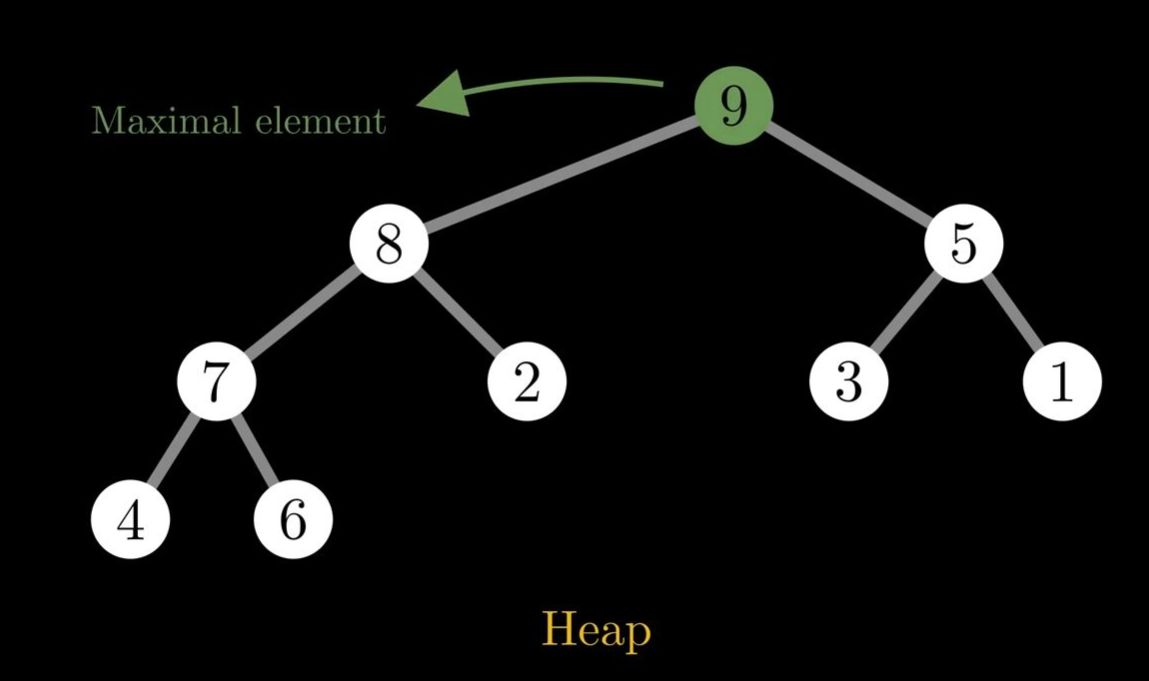
A Max Heap is a binary tree (but not a binary search tree important) with the property that each node key is greater than or equal to the key of its children.
A Min Heap is a binary tree where each node key is less than or equal to the keys of its children.
Representation of Graph#
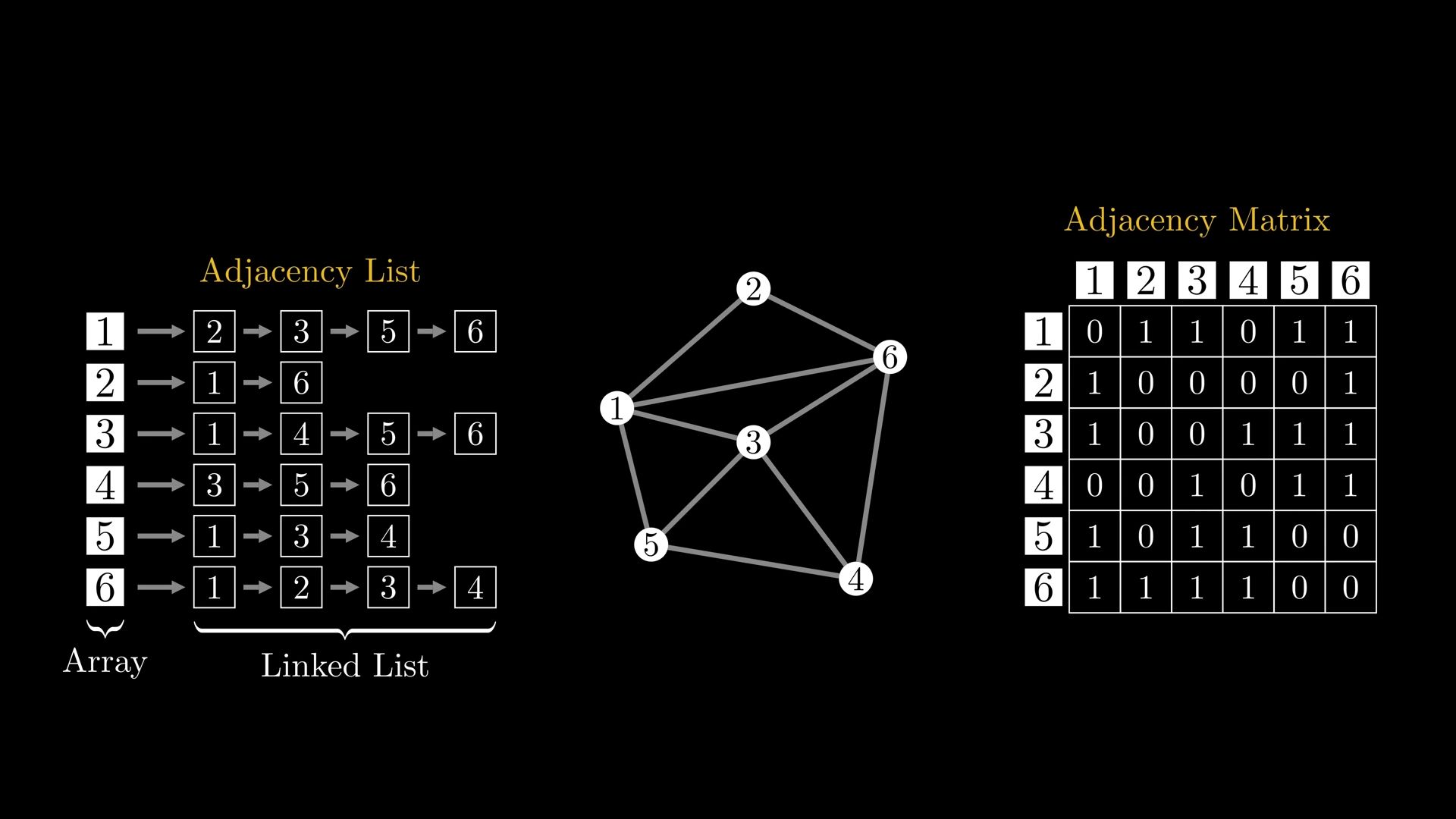
Adjacency List is more memory efficient.